在一次数学竞赛中,10名学生的成绩(单位:分)分别为70,90,80,50,80,80,60,100,90,80.求这些学生的平均成绩.
观察下列算式:①1×3-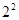 =3-4=-1;②2×4-
=3-4=-1;②2×4- =8-9=-1;
=8-9=-1;
③3×5-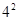 =15-16=-1;④;……
=15-16=-1;④;……
(1)请你按以上规律写出第4个算式;
(2)请你把这个规律用含n的式子表示出来:=;
(3)你认为(2)中所写的式子一定成立吗?说明理由。
如图,AD∥BC,∠A=94°,∠D=106°,BE、CE分别是∠ABC和∠BCD的角平分线,求∠BEC的度数。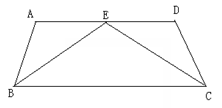
画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸中将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
(1)请画出平移后的△A′B′C′.
(2)若连接AA′,CC′,则这两条线段之间的关系是________.
(3)利用网格画出△ABC 中AC边上的中线BD
(4)利用网格画出△ABC 中AB边上的高CE.
(5)△A′B′C′的面积为。
因式分解:(每题3分,共12分)
(1)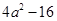
(2)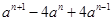
(3)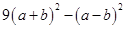
(4)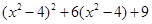
先化简,再求值:(每题4分,共12分)
(1)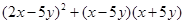 ,其中
,其中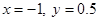
(2)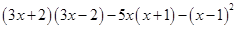 ,其中
,其中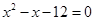
(3)已知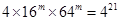 ,求
,求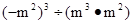 的值。
的值。