某景区内的环形路是边长为800米的正方形ABCD，如图1和图-优题课

某景区内的环形路是边长为800米的正方形ABCD，如图1和图2．现有1号、2号两游览车分别从出口A和景点C同时出发，1号车顺时针、2号车逆时针沿环形路连续循环行驶．供游客随时免费乘车(上、下车的时间忽略不计)，两车速度均为200米／分．
探究设行驶时间为t分．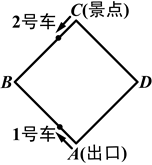

(1)当0≤t≤8时，分别写出1号车、2号车在左半环线离出口A的路程y₁，y₂(米)与t(分)的函数关系式，并求出当两车相距的路程是400米时t的值；
(2)t为何值时，1号车第三次恰好经过景点C？并直接写出这一段时间内它与2号车相遇过的次数．
发现如图2，游客甲在BC上的一点K(不与点B，C重合)处候车，准备乘车到出口A．设CK＝x米．
情况一：若他刚好错过2号车，便搭乘即将到来的1号车；
情况二：若他刚好错过1号车，便搭乘即将到来的2号车．
比较哪种情况用时较多．(含候车时间)

决策已知游客乙在DA上从D向出口A走去，步行的速度是50米／分．当行进到DA上一点P(不与点D，A重合)时，刚好与2号车迎面相遇．
(1)他发现，乘1号车会比乘2号车到出口A用时少，请你简要说明理由；
(2)设PA＝s(0＜s＜800)米．若他想尽快到达出口A，根据s的大小，在等候乘1号车还是步行这两种方式中，他该如何选择？

科目数学题型解答题难度中等

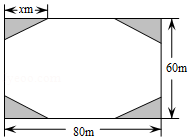
结合西昌市创建文明城市要求，某小区业主委员会决定把一块长 $80 m$ ，宽 $60 m$ 的矩形空地建成花园小广场，设计方案如图所示，阴影区域为绿化区（四块绿化区为全等的直角三角形），空白区域为活动区，且四周出口宽度一样，其宽度不小于 $36 m$ ，不大于 $44 m$ ，预计活动区造价60元 $/ m^{2}$ ，绿化区造价50元 $/ m^{2}$ ，设绿化区域较长直角边为 $xm$ ．

（1）用含 $x$ 的代数式表示出口的宽度；

（2）求工程总造价 $y$ 与 $x$ 的函数关系式，并直接写出 $x$ 的取值范围；

（3）如果业主委员会投资28.4万元，能否完成全部工程？若能，请写出 $x$ 为整数的所有工程方案；若不能，请说明理由．

（4）业主委员会决定在（3）设计的方案中，按最省钱的一种方案，先对四个绿化区域进行绿化，在实际施工中，每天比原计划多绿化 $11 m^{2}$ ，结果提前4天完成四个区域的绿化任务，问原计划每天绿化多少 $m^{2}$ ．

阅读材料：基本不等式 $\sqrt{ab} ⩽ \frac{a + b}{2} (a > 0, b > 0)$ ，当且仅当 $a = b$ 时，等号成立．其中我们把 $\frac{a + b}{2}$ 叫做正数 $a$ 、 $b$ 的算术平均数， $\sqrt{ab}$ 叫做正数 $a$ 、 $b$ 的几何平均数，它是解决最大（小 $)$ 值问题的有力工具．

例如：在 $x > 0$ 的条件下，当 $x$ 为何值时， $x + \frac{1}{x}$ 有最小值，最小值是多少？

解： $∵ x > 0$ ， $\frac{1}{x} > 0 ∴ \frac{x + \frac{1}{x}}{2} ⩾ \sqrt{x \cdot \frac{1}{x}}$ 即是 $x + \frac{1}{x} ⩾ 2 \sqrt{x \cdot \frac{1}{x}}$

$∴ x + \frac{1}{x} ⩾ 2$

当且仅当 $x = \frac{1}{x}$ 即 $x = 1$ 时， $x + \frac{1}{x}$ 有最小值，最小值为2．

请根据阅读材料解答下列问题

（1）若 $x > 0$ ，函数 $y = 2 x + \frac{1}{x}$ ，当 $x$ 为何值时，函数有最值，并求出其最值．

（2）当 $x > 0$ 时，式子 $x^{2} + 1 + \frac{1}{x^{2} + 1} ⩾ 2$ 成立吗？请说明理由．

已知： $ΔABC$ 内接于 $⊙ O$ ， $AB$ 是 $⊙ O$ 的直径，作 $EG ⊥ AB$ 于 $H$ ，交 $BC$ 于 $F$ ，延长 $GE$ 交直线 $MC$ 于 $D$ ，且 $∠ MCA = ∠ B$ ，求证：

（1） $MC$ 是 $⊙ O$ 的切线；

（2） $ΔDCF$ 是等腰三角形．

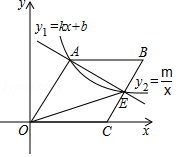
$▱ ABCO$ 在平面直角坐标系中的位置如图所示，直线 $y_{1} = kx + b$ 与双曲线 $y_{2} = \frac{m}{x} (m > 0)$ 在第一象限的图象相交于 $A$ 、 $E$ 两点，且 $A (3, 4)$ ， $E$ 是 $BC$ 的中点．

（1）连接 $OE$ ，若 $ΔABE$ 的面积为 $S_{1}$ ， $ΔOCE$ 的面积为 $S_{2}$ ，则 $S_{1}$ 　 $=$ 　 $S_{2}$ （直接填“ $>$ ”“ $<$ ”或“ $=$ ” $)$ ；

（2）求 $y_{1}$ 和 $y_{2}$ 的解析式；

（3）请直接写出当 $x$ 取何值时 $y_{1} > y_{2}$ ．

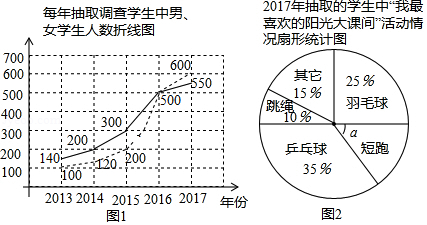
西昌市教科知局从2013年起每年对全市所有中学生进行“我最喜欢的阳光大课间活动”抽样调查（被调查学生每人只能选一项），并将抽样调查的数据绘制成图1、图2两幅统计图，根据统计图提供的信息解答下列问题：

（1）　　年抽取的调查人数最少；　　年抽取的调查人数中男生、女生人数相等；

（2）求图2中“短跑”在扇形图中所占的圆心角 $α$ 的度数；

（3）2017年抽取的学生中，喜欢羽毛球和短跑的学生共有多少人？

（4）如果2017年全市共有3.4万名中学生，请你估计我市2017年喜欢乒乓球和羽毛球两项运动的大约有多少人？