如图，将两块腰长相等的三角尺（△ABC和△DEF，其中∠ACB=∠DFE=90°）
置于水平面上，直角边BC=EF=1cm，且始终紧贴在水平直线
上．
（1）在图①中，当边DF与边AC重合时，AB与AE的大小关系是__________；
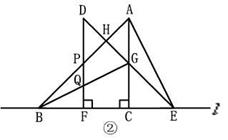
（2）将三角板ABC以1cm/s的速度从图①的位置沿直线向右平移，设平移的时间为t (s)，如图
②所示．当0＜t＜1时，DE分别交AC、AB于点G、H，DF分别交AB、BG于点P、Q，
连结BG、AE．
①求证：BG=AE；
②在平移过程中，是否存在某时刻t，使得以点D、G、Q为顶点的三角形是等腰三角形？若存在，请求出t的值；若不存在，请说明理由．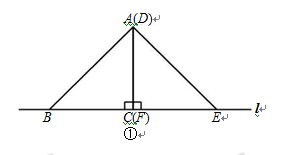
已知函数y＝(2m＋1)x＋m－3
（1）若函数图象经过原点，求m的值；
（2）若函数的图象平行直线y＝3x－3，求m的值；
（3）若这个函数是一次函数，且y随着x的增大而减小，求m的取值范围．
已知一次函数的图像经过A（2，4），B（0，2）两点，且与
轴交于点C，求：
（1）一次函数的解析式；（2）△AOC的面积.
（1）请画出
关于
轴对称的
（其中
分别是
的对应点，不写画法）；
（2）直接写出三点的坐标：
．
（3）求△ABC的面积是多少？
（1）计算：
（2）计算：
如图，直线L：
与x轴、y轴分别交于A、B两点，在y轴上有一点
C（0，4）,动点M从A点以每秒1个单位的速度沿x轴向左移动。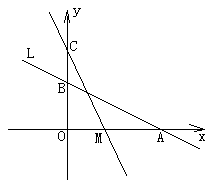
（1）求A、B两点的坐标；
（2）求△COM的面积S与M的移动时间t之间的函数关系式；
（3）当t为何值时△COM≌△AOB，并求此时M点的坐标。