不等式 的解集为.
的解集为.
已知曲线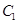 的参数方程是
的参数方程是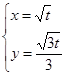
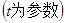 ,以坐标原点为极点,
,以坐标原点为极点,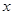 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线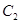 的极坐标方程是
的极坐标方程是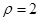 ,则
,则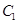 与
与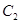 交点的直角坐标为________.
交点的直角坐标为________.
已知AB,BC是圆O的两条弦,AO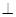 BC,AB=
BC,AB=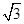 ,BC=
,BC=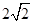 ,则圆O的半径等于________.
,则圆O的半径等于________.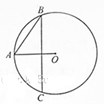
以 表示值域为R的函数组成的集合,
表示值域为R的函数组成的集合, 表示具有如下性质的函数
表示具有如下性质的函数 组成的集合:对于函数
组成的集合:对于函数 ,存在一个正数
,存在一个正数 ,使得函数
,使得函数 的值域包含于区间
的值域包含于区间 。例如,当
。例如,当 ,
, 时,
时, ,
, 。现有如下命题:
。现有如下命题:
①设函数 的定义域为
的定义域为 ,则“
,则“ ”的充要条件是“
”的充要条件是“ ,
, ,
, ”;
”;
②函数 的充要条件是
的充要条件是 有最大值和最小值;
有最大值和最小值;
③若函数 ,
, 的定义域相同,且
的定义域相同,且 ,
, ,则
,则
④若函数 (
( ,
, )有最大值,则
)有最大值,则 。
。
其中的真命题有__________________.(写出所有真命题的序号).
过点 作斜率为
作斜率为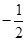 的直线与椭圆
的直线与椭圆 :
: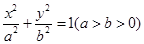 相交于A,B,若M是线段AB的中点,则椭圆C的离心率为.
相交于A,B,若M是线段AB的中点,则椭圆C的离心率为.