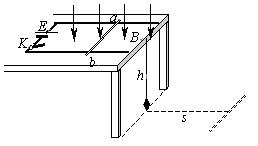
如图所示,水平桌面上放着一对平行金属导轨,左端与一电源相连,中间还串有一开关K。导轨上放着一根金属棒ab,空间存在着垂直导轨平面向下的匀强磁场.已知两导轨间距为d,电源电动势为E,导轨电阻及电源内阻均不计,ab棒的电阻为R,质量为m,棒与导轨间摩擦不计.闭合开关K,ab棒向右运动并从桌边水平飞出,已知桌面离地高度为h,金属棒落地点的水平位移为s。下面的结论中正确( )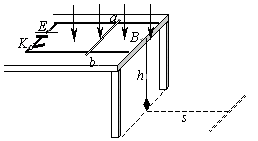

A.开始时ab棒离导轨右端的距离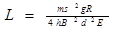 |
B.磁场力对ab棒所做的功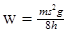 |
C.磁场力对ab棒的冲量大小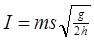 |
D.ab棒在导轨上运动时间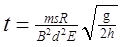 |
如图所示,小球以初速度为v0从光滑斜面底部向上滑,恰能到达最大高度为h的斜面顶部。右图中A是内轨半径大于h的光滑轨道、B是内轨半径小于h的光滑轨道、C是内轨直径等于h光滑轨道、D是斜抛无轨道的运动的小球。小球在底端时的初速度都为v0,则小球在以上四种情况中能到达高度h的是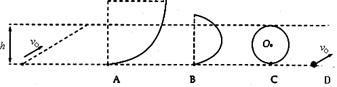
静止在粗糙水平面上的物块A受方向始终水平向右的拉力作用下做直线运动,t=4s时停下,其速度—时间图象如图所示,已知物块A与水平面间的动摩擦因数处处相同,下列判断正确的是
| A.全过程中拉力做的功等于物块克服摩擦力做的功 |
| B.全过程拉力做的功等于零 |
| C.t=2s时刻拉力瞬时功率,为整个过程拉力功率的最大值 |
| D.t=1s到t=3s这段时间内拉力不做功 |
使物体脱离某星球的引力束缚,不再绕星球运行,从星球表面发射所需的最小速度称为第二宇宙速度,星球的第二宇宙速度v2与第一宇宙速度v1的关系是 1。已知某星球的半径为r,它表面的重力加速度为地球表面重力加速度g的
1。已知某星球的半径为r,它表面的重力加速度为地球表面重力加速度g的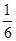 。不计其他星球的影响,则该星球的第二宇宙速度为
。不计其他星球的影响,则该星球的第二宇宙速度为
A.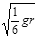 |
B.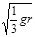 |
C.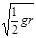 |
D.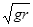 |
质量为m的物体,从距地面h高处由静止开始以加速度a=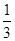 g竖直下落到地面,在此过程
g竖直下落到地面,在此过程
A.物体的动能增加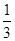 mgh mgh |
B.物体的重力势能减少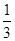 mgh mgh |
C.物体的机械能减少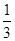 mgh mgh |
| D.物体的机械能保持不变 |
经长期观测人们在宇宙中已经发现了“双星系统”。“双星系统”由两颗相距较近的恒星组成,每个恒星的线度远小于两个星体之间的距离,而且双星系统一般远离其他天体。如图,两颗星球组成的双星,在相互之间的万有引力作用下,绕连线上的O点做周期相同的匀速圆周运动。现测得两颗星之间的距离为L,质量之比为m1∶m2 =3∶2,则可知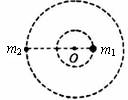
| A.m1、m2做圆周运动的线速度之比为3∶2 |
| B.m1、m2做圆周运动的角速度之比为3∶2 |
C.m1做圆周运动的半径为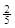 L L |
D.m2做圆周运动的半径为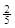 L L |