在如图所示的xoy,平面直角坐标系中,一足够长绝缘薄板正好和x轴的正半轴重合,在y>a和y<-a的区域内均分布着方向垂直纸面向里的相同的匀强磁场。一带正电粒子,从y轴上的(0,a)点以速度v沿与y轴负向成45°角出射。带电粒子与挡板碰撞前后,x方向的分速度不变,y方向的分速度反向、大小不变。已知粒子质量为m,电荷量为q,磁感应强度的大小 。不计粒子的重力。
。不计粒子的重力。
(1)求粒子进入下方磁场后第一次打在绝缘板上的位置
(2)若在绝缘板上的合适位置开一小孔,粒子穿过后能再次回到出发点。写出在板上开这一小孔可能的位置坐标(不需要写出过程)
(3)在满足(2)的情况下,求粒子从出射到再次返回出发点的时间
用绳拴住木棒AB的A端,使木棒在竖直方向上静止不动.在木棒A端正下方有一点C距A端0.8 m.若把绳轻轻剪断,测得A、B两端通过C点的时间差是0.2 s.重力加速度g="10" m/s2,求木棒AB的长度.
一辆执勤的警车停在公路旁,当警员发现从他身边以8m/s的速度匀速行驶的货车有违章行为时,决定前去追赶 ,警车以加速度a=2m/s2做匀加速直线运动追赶货车,试问:
(1)若警车一直匀加速追赶,要多长时间才能追上违章的货车?
(2)在警车追上货车之前,两车之间的最大距离是多少?
汽车先以a1=0.5m/s2的加速度由静止开始做匀加速直线运动,在20s末改做匀速直线运动,当匀速运动持续10s后,因遇到障碍汽车便紧急刹车,已知刹车的加速度为a2=-2m/s2,求:
(1)汽车匀速运动时的速度大小;
(2)汽车刹车后的6s内所通过的位移;
(3)在坐标图上画出该汽车运动全过程的速度一时间图象。
如图所示,电阻R3=4 Ω,电表为理想表.开始时R1、R2、R3中都有电流通过,电压表示数为2 V,电流表示数为0.75 A.后来三个电阻中有一个发生断路,使电压表示数变为3.2 V,电流表示数变为0.8 A.
(1)哪个电阻断路?
(2)求电阻R1、R2的阻值各为多少?
(3)电源电动势和内阻各为多少?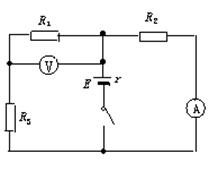
如图所示的电路中已知电源电动势E=36V,内电阻r=2Ω,R1=20Ω,每盏灯额定功率都是2W,额定电压也相同。当K闭合将电阻箱R2调到R2=14Ω时,两灯都正常发光;当K断开后为使L2仍正常发光,求R2应调到何值?