2015“两相和”杯群星演唱会在我市体育馆进行，市文化局、广电局在策划本次活动，在与单位协商团购票时推出两种方案．设购买门票数为x（张），总费用为y（元）．
方案一：若单位赞助广告费8000元，则该单位所购门票的价格为每张50元；（总费用＝广告赞助费+门票费）
方案二：直接购买门票方式如图所示．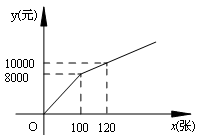
解答下列问题：
（1）方案一中，y与x的函数关系式为 ；方案二中，当0≤x≤100时，y与x的函数关系式为 ，当x＞100时，y与x的函数关系式为 ；
（2）甲、乙两单位分别采用方案一、方案二购买本场演唱会门票共700张，花去总费用计56000元，求甲、乙两单位各购买门票多少张？
（本题5分）列方程解应用题
甲、乙两站相距480千米，货车与客车同时从甲站出发开往乙站。已知客车的速度是货车的2.5倍,结果客车比货车早6小时到达乙站,求两种车的速度各是多少。
（本题5分）a为何值时，关于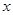
的方程
有增根？
（本题8分，每小题4分）解方程：
（1）
（2）
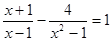
(12分)抛物线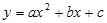
中，b，c是非零常数，无论a为何值（0除外），其顶点M一定在直线y=kx+1上，这条直线和x轴，y轴分别交于点E，A，且OA=OE.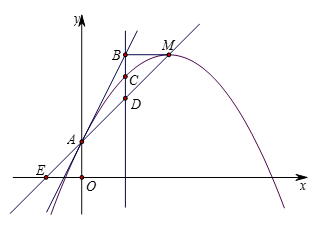
（1）求k的值；
（2）求证：这条抛物线经过点A；
（3）经过点A的另一条直线y=mx+n和这条抛物线只有一个公共点，经过点M作x轴的平行线和直线y=mx+n交于点B，经过点B作x轴的垂线和这条抛物线交于点C，和直线y=kx+1交于点D，探索CD和BC的数量关系.
正方形ABCD中，将一个直角三角板的直角顶点与点A重合，一条直角边与边BC交于点E（点E不与点B和点C重合），另一条直角边与边CD的延长线交于点F.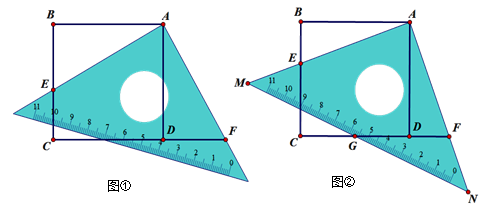
（1）如图①，求证：AE="AF;"
（2）如图②，此直角三角板有一个角是45°，它的斜边MN与边CD交于G，且点G是斜边MN的中点，连接EG，求证：EG="BE+DG;"
（3）在（2）的条件下，如果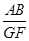
= 
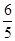，那么点G是否一定是边CD的中点?请说明你的理由.