如图所示，横截面(纸面)为△ABC的三棱镜置于空气中，顶角∠A=60°．纸面内一细光束以入射角i射入AB面，直接到达AC面并射出，光束在通过三棱镜时出射光与入射光的夹角为
(偏向角)．改变入射角i，当i=i0时，从AC面射出的光束的折射角也为i0，理论计算表明在此条件下偏向角有最小值
．求三棱镜的折射率n．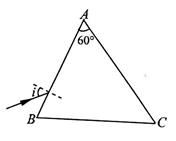
甲、乙两船在静水中航行的速度分别为V甲和V乙，两船从同一渡口向河对岸划去．已知甲船以最短时间过河，乙船以最短航程过河，结果两船抵达对岸的地点恰好相同，则甲、乙两船渡河所用时间之比t甲和t乙为多少？
河宽d＝20cm，水流速度v水＝1m/s，船在静水中的划速为v划＝2m/s，求：
（1）要使船能垂直渡过河去，划船速度的方向？
（2）要使船能在最短的时间过河，划船速度的方向？最短时间是多少？
一探照灯照射在云层底面上，这底面是与地面平行的平面，如图所示，云层底面高h，探照灯以匀角速度ω在竖直平面内转动．当光束与竖直线夹角为θ时，求此刻云层底面上光点的移动速度．
如图，以速度v沿竖直杆匀速下滑的物体A，用钢绳通过定滑轮拉物体B在水平面上运动，当绳与水平面夹角为θ时，物体B运动速率为多少？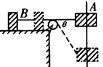
一个质量为0.5kg的物体放在水平面上，它与水平面间的动摩擦因数为μ＝0.2，从静止开始受水平力而运动；物体在前5s内受到一个正东方向、大小为F1＝2.0N的水平恒力作用，在第5s末撤去F1，同时物体进入光滑水平面并受到一个正北方向、大小为F2＝0.5N的水平恒力，作用时间为10s．g＝10m/s2，那么：
（1）该物体在前5s和后10s各做什么运动？
（2）求第5s末和第15s末物体的速度．