如图所示，AKD为竖直平面内固定的光滑绝缘轨道，轨道间均平滑连接，AK段水平，其间分布有一水平向右的匀强电场I。PQ为同一竖直面内的固定光滑水平轨道。自D点向右宽度L=0.7m的空间，分布有水平向右、场强大小E=1.4×105N/C的匀强电场II。质量m2=0.1kg、长度也为L的不带电绝缘平板，静止在PQ上并恰好处于电场II中，板的上表面与弧形轨道相切于D点。AK轨道上一带正电的小物体从电场I的左边界由静止开始运动，并在D点以速度v=1m/s滑上平板。已知小物体的质量m1=10－2kg，电荷量q=＋10－7C,与平板间的动摩擦因数
,AK与D点的垂直距离为h=0.3m，小物体离开电场II时速度比平板的大、小物体始终在平板上。设小物体电荷量保持不变且视为质点，取g=10m/s2。求：
（1）电场I左右边界的电势差；
（2）小物体从离开电场II开始，到平板速度最大时，所需要的时间。
某同学在测定一厚度均匀的圆形玻璃的折射率时，先在白纸上作一与圆形玻璃同半径的圆，圆心为O，将圆形玻璃平放在白纸上，使其边界与所画的圆重合，在玻璃一侧竖直插两枚大头针P1和P2，在另一侧再先后插两枚大头针P3和P4，使从另一侧隔着玻璃观察时，大头针P4、P3和P2、P1的像恰在一直线上，移去圆形玻璃和大头针后，在图13-1-11中画出：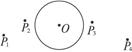
图13-1-11
（1）沿P1、P2连线方向的入射光线通过圆形玻璃后的传播方向；
（2）光线在玻璃内的传播方向；
（3）过光线的入射点作法线，标出入射角i和折射角r；
（4）写出计算玻璃折射率的公式.
试根据平抛运动原理设计测量弹射器弹丸出射初速的实验方法.
提供的实验器材：
弹射器（含弹丸，见右图）；
铁架台（带有夹具）；米尺.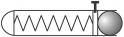
（1）画出实验示意图.
（2）在安装弹射器时应注意：____________.
（3）实验中需要测量的量（并在示意图中用字母标出）：____________.
（4）由于弹射器每次射出的弹丸初速不可能完全相等，在实验中应采取的方法是：____________.
（5）计算公式：____________.
如图是欧姆表的工作原理图。
（1）若表头的满偏电流为Ig=500μA，干电池的电动势为1.5Ｖ，把灵敏电流表的电流刻度值对应的欧姆表电阻值填在下表中：
| 电流刻度 |
0 |
50μA |
100μA |
200μA |
250μA |
300μA |
400μA |
500μA |
| 电阻刻度 |
（2）这只欧姆表的总内阻为Ω，表针偏转到满刻度的1/3时，待测电阻为Ω. 
一个物体从H高处自由落下，经过最后196 m所用的时间是4 s，求物体下落H高所用的总时间T和高度H是多少？（取g="9.8" m/s2,空气阻力不计）
如图8所示，滑块A以一定初速度沿木板B向右滑动，木板B在地面上保持静止，已知滑块A的质量为m1,木板B的质量为m2,A、B间的动摩擦因数为μ1，B与地面间的动摩擦因数为μ2,则在A滑动过程中，A受到的摩擦力为多大？木板B受到地面的摩擦力又为多大？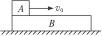
图8