在用数学归纳法证明f（n）=
+
+…+
＜1（n∈N*，n≥3）的过程中：假设当n=k（k∈N*，k≥3）时，不等式f（k）＜1成立，则需证当n=k+1时，f（k+1）＜1也成立．若f（k+1）=f（k）+g（k），则g（k）=（）
A． + |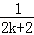
B． + ﹣ |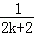
C．﹣ |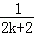
D．﹣ |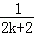
用数学归纳法证明1+2+3+…+n3=
，则当n=k+1时，左端应在n=k的基础上加上（）
| A．k3+1 |
| B．（k+1）3 |
C． |
| D．（k3+1）+（k3+2）+（k3+3）+…+（k3+1）3 |
若a＜b＜c，x＜y＜z，则下列各式中值最大的一个是（）
| A．ax+cy+bz | B．bx+ay+cz |
| C．bx+cy+az | D．ax+by+cz |
设变量x，y满足|x﹣2|+|y﹣2|≤1，则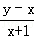
的最大值为（）
A． |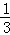
B． |
C．﹣ |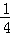
D． |
已知a，b，c∈R，则2a2+3b2+6c2=1是a+b+c∈[﹣1，1]的（）
| A．充分不必要条件 | B．必要不充分条件 |
| C．充分必要条件 | D．既不充分也不必要条件 |
在
上是单调函数，则ω应满足的条件是（