如图, 已知:BF=DE,∠1=2,∠3=∠4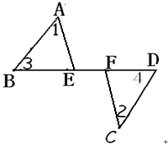
求证:AE=CF.
证明:
因式分解: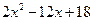
已知:在△ABC中,BC=a,AC=b,以AB为边作等边三角形ABD. 探究下列问题:
(1)如图1,当点D与点C位于直线AB的两侧时,a=b=3,且∠ACB=60°,则CD=;
(2)如图2,当点D与点C位于直线AB的同侧时,a=b=6,且∠ACB=90°,则CD=;
(3)如图3,当∠ACB变化,且点D与点C位于直线AB的两侧时,求 CD的最大值及相应的∠ACB的度数.


图1图2图3
已知:如图,在□ EFGH中,点F的坐标是(-2,-1),∠EFG=45°.
(1)求点H的坐标;
(2)抛物线 经过点E、G、H,现将
经过点E、G、H,现将 向左平移使之
向左平移使之 经过点F,得到抛物线
经过点F,得到抛物线 ,求抛物线
,求抛物线 的解析式;
的解析式;
(3)若抛物线 与y轴交于点A,点P在抛物线
与y轴交于点A,点P在抛物线 的对称轴上运动.请问:是否存在以AG为腰的等腰三角形AGP?若存在,求出点P的坐标;若不存在,请说明理由.
的对称轴上运动.请问:是否存在以AG为腰的等腰三角形AGP?若存在,求出点P的坐标;若不存在,请说明理由.
已知: 反比例函数
反比例函数 经过点B(1,1) .
经过点B(1,1) .
(1)求该反比例函数解析式;
(2) 联结OB,再把点
联结OB,再把点 A(2,0)与点B联结,将△OAB绕点O按顺时针方向旋转135°得到△O
A(2,0)与点B联结,将△OAB绕点O按顺时针方向旋转135°得到△O ,写出
,写出 的中点P的坐标,试判断点P是否在此双曲线上,并说明理由;
的中点P的坐标,试判断点P是否在此双曲线上,并说明理由;
(3)若该反比例函数图象上有一点F(m, )(其中m>0),在线段OF上任取一点E,
)(其中m>0),在线段OF上任取一点E,
设E点的纵坐标为n,过F点作FM⊥x轴于点M,联结EM,使△OEM的面积是 ,求代数式
,求代数式 的值.
的值.