如图,C是以AB为直径的 上一点,过点O作OE⊥AC于点E,过点A作⊙O的切线交OE的延长线于点F,连接CF并延长交BA的延长线于点P.
上一点,过点O作OE⊥AC于点E,过点A作⊙O的切线交OE的延长线于点F,连接CF并延长交BA的延长线于点P.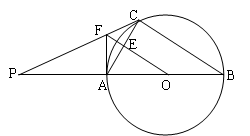
(1)求证:PC是⊙O的切线;
(2)若AF=1,OA=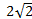 , 求PC的长。
, 求PC的长。
荣庆公司计划从商店购买同一品牌的台灯和手电筒,已知购买一个台灯比购买一个手电筒多用20元,若用400元购买台灯和用160元购买手电筒,则购买台灯的个数是购买手电筒个数的一半.
(1)求购买该品牌一个台灯、一个手电筒各需要多少元?
(2)经商谈,商店给予荣庆公司购买一个该品牌台灯赠送一个该品牌手电筒的优惠,如果荣庆公司需要手电筒的个数是台灯个数的2倍还多8个,且该公司购买台灯和手电筒的总费用不超过670元,那么荣庆公司最多可购买多少个该品牌台灯?
如图,⊙O是△ABC的外接圆,弦BD交AC于点E,连接CD,且AE=DE,BC=CE.
(1)求∠ACB的度数;
(2)过点O作OF⊥AC于点F,延长FO交BE于点G,DE=3,EG=2,求AB的长.
如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).
君畅中学计划购买一些文具送给学生,为此学校决定围绕“在笔袋、圆规、直尺、钢笔四种文具中,你最需要的文具是什么?(必选且只选一种)”的问题,在全校满园内随机抽取部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的统计图,请你根据以上信息回答下列问题: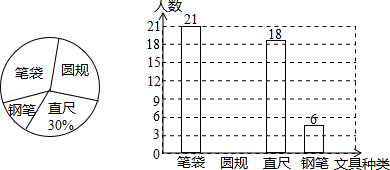
(1)在这次调查中,最需要圆规的学生有多少名?并补全条形统计图;
(2)如果全校有970名学生,请你估计全校学生中最需要钢笔的学生有多少名?
如图,方格纸中每个小正方形的边长均为1,四边形ABCD的四个顶点都在小正方形的顶点上,点E在BC边上,且点E在小正方形的顶点上,连接AE.
(1)在图中画出△AEF,使△AEF与△AEB关于直线AE对称,点F与点B是对称点;
(2)请直接写出△AEF与四边形ABCD重叠部分的面积.