已知四棱锥P-ABCD,底面ABCD是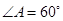 的菱形,又
的菱形,又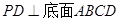 ,且PD=CD,点M、N分别是棱AD、PC的中点.
,且PD=CD,点M、N分别是棱AD、PC的中点.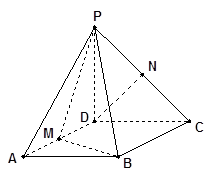
(Ⅰ)证明:DN//平面PMB;
(Ⅱ)证明:平面PMB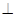 平面PAD;
平面PAD;
为了比较注射A,B两种药物后产生的皮肤疱疹的面积,选200只家兔做实验,将这200只家兔随机地分成两组。每组100只,其中一组注射药物A,另一组注射药物B。下表1和表2分别是注射药物A和药物B后的实验结果。(疱疹面积单位: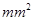 )表1:注射药物A后皮肤疱疹面积的频数分布表
)表1:注射药物A后皮肤疱疹面积的频数分布表
| 疱疹面积 |
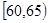 |
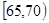 |
 |
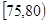 |
| 频数 |
30 |
40 |
20 |
10 |
表2:注射药物B后皮肤疱疹面积的频数分布表
| 疱疹面积 |
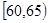 |
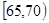 |
 |
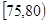 |
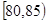 |
| 频数 |
10 |
25 |
20 |
30 |
15 |
(1)完成下面频率分布直方图,并比较注射两种药物后疱疹面积的中位数大小;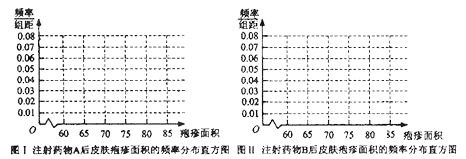
(2)完成下面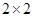 列联表,并回答能否有99.9%的把握认为“注射药物A后的疱疹面积与注射药物B后的疱疹面积有差异”。 (结果保留4位有效数字)
列联表,并回答能否有99.9%的把握认为“注射药物A后的疱疹面积与注射药物B后的疱疹面积有差异”。 (结果保留4位有效数字)
| |
疱疹面积小于70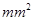 |
疱疹面积不小于70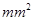 |
合计 |
| 注射药物A |
a= |
b= |
|
| 注射药物B |
c= |
d= |
|
| 合计 |
n= |
附: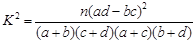
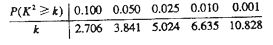
已知椭圆 的离心率为
的离心率为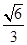 ,右焦点为(
,右焦点为(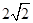 ,0),斜率为1的直线
,0),斜率为1的直线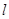 与椭圆G交与A、B两点,以AB为底边作等腰三角形,顶点为P(-3,2).
与椭圆G交与A、B两点,以AB为底边作等腰三角形,顶点为P(-3,2).
(1)求椭圆G的方程;(2)求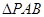 的面积.
的面积.
求两变量间的回归方程.
| 价格x |
14 |
16 |
18 |
20 |
22 |
| 需求量Y |
12 |
10 |
7 |
5 |
3 |
求出Y对X的回归直线方程,并说明拟合效果的好坏。(其中 )
)
已知x,y,z是互不相等的正数,且x+y+z=1,求证: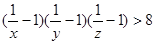 .
.
已知函数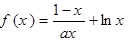
(1)若函数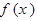 在
在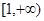 上为增函数,求正实数
上为增函数,求正实数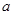 的取值范围;
的取值范围;
(2)当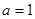 时,求函数
时,求函数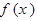 在
在 上的最值;
上的最值;
(3)当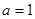 时,对大于1的任意正整数
时,对大于1的任意正整数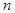 ,试比较
,试比较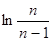 与
与 的大小关系.
的大小关系.