阅读、操作与探究:
小亮发现一种方法,可以借助某些直角三角形画矩形,使矩形邻边比的最简形式(如4:6的最简形式为2:3)为两个连续自然数的比,具体操作如下:
如图1,Rt△ABC中,BC,AC,AB的长分别为3,4,5,先以点B为圆心,线段BA的长为半径画弧,交CB的延长线于点D,再过D,A两点分别作AC,CD的平行线,交于点E.得到矩形ACDE,则矩形ACDE的邻边比为 .
请仿照小亮的方法解决下列问题:
(1)如图2,已知Rt△FGH中,GH:GF:FH= 5:12:13,请你在图2中画一个矩形,使所画矩形邻边比的最简形式为两个连续自然数的比,并写出这个比值;
(2)若已知直角三角形的三边比为 (n为正整数),则所画矩形(邻边比的最简形式为两个连续自然数的比)的邻边比为 .
(n为正整数),则所画矩形(邻边比的最简形式为两个连续自然数的比)的邻边比为 .
如图,在同一个平面内有四个点A、B、C、D.
①画射线CD;②画直线AD;③连接AB;④直线BD与直线AC相交于点O.
化简并求值:6( a2﹣2ab)﹣2(6a2﹣5ab),其中a=﹣
a2﹣2ab)﹣2(6a2﹣5ab),其中a=﹣ ,b=2.
,b=2.
解方程:
(1)2(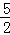 x﹣4)=1﹣2x;
x﹣4)=1﹣2x;
(2)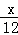 ﹣3=
﹣3=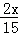 .
.
某单位在五月份准备组织部分员工到北京旅游,现联系了甲、乙两家旅行社,两家旅行社报价均为2000元/人,两家旅行社同时都对10人以上的团体推出了优惠举措:甲旅行社对每位员工七五折优惠;而乙旅行社是免去一位带队管理员工的费用,其余员工八折优惠.
(1)如果设参加旅游的员工共有a(a>10)人,则甲旅行社的费用为 元,乙旅行社的费用为 元;(用含a的代数式表示,并化简.)
(2)假如这个单位现组织包括管理员工在内的共20名员工到北京旅游,该单位选择哪一家旅行社比较优惠?请说明理由.
(3)如果计划在五月份外出旅游七天,设最中间一天的日期为a,则这七天的日期之和为 .(用含a的代数式表示,并化简.)
(4)假如这七天的日期之和为63的倍数,则他们可能于五月几号出发?(写出所有符合条件的可能性,并写出简单的计算过程.)
观察下列各式:
﹣1× =﹣1+
=﹣1+
﹣ ×
× =﹣
=﹣ +
+
﹣ ×
× =﹣
=﹣ +
+
…
(1)你能探索出什么规律?(用文字或表达式)
(2)试运用你发现的规律计算:
(﹣1× )+(﹣
)+(﹣ ×
× )+(﹣
)+(﹣ ×
× )+…+(﹣
)+…+(﹣ ×
× )+(﹣
)+(﹣ ×
× )
)