(本小题满分12分)如下图所示,从参加环保知识竞赛的学生中抽出60名,将其成绩整理后画出的频率分布直方图,观察图形,回答下列问题:
(Ⅰ) 这一组的频率和频数分别为多少?
这一组的频率和频数分别为多少?
(Ⅱ)估计这次环保知识竞赛的平均成绩。
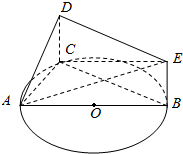
如图,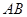 是圆
是圆 的直径,
的直径, 是圆
是圆 上异于
上异于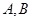 的一个动点,
的一个动点,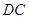 垂直于圆
垂直于圆 所在的平面,
所在的平面,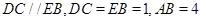 .
.
(1)求证: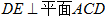 ;
;
(2)若 ,求平面
,求平面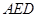 与平面
与平面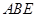 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
某校校庆,各届校友纷至沓来,某班共来了 位校友(
位校友( ),其中女校友6位,组委会对这
),其中女校友6位,组委会对这 位校友登记制作了一份校友名单,现随机从中选出2位校友代表,若选出的2位校友是一男一女,则称为“最佳组合” ..
位校友登记制作了一份校友名单,现随机从中选出2位校友代表,若选出的2位校友是一男一女,则称为“最佳组合” ..
(1)若随机选出的2位校友代表为“最佳组合”的概率不小于 ,求
,求 的最大值;
的最大值;
(2)当 时,设选出的2 位校友代表中女校友人数为
时,设选出的2 位校友代表中女校友人数为 ,求随机变量
,求随机变量 的分布列和数学期望
的分布列和数学期望 .
.
已知数列 的前
的前 项和为
项和为 ,且
,且 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前
的前 项和
项和 .
.
选修4-5:不等式选讲
已知函数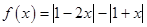
(1)解不等式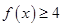 ;
;
(2)若函数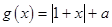 的图象恒在函数
的图象恒在函数 的图象的上方,求实数
的图象的上方,求实数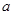 的取值范围.
的取值范围.
选修4-4:极坐标与参数方程
在极坐标系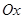 中,直线
中,直线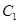 的极坐标方程为
的极坐标方程为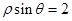 ,
,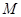 是
是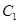 上任意一点,点
上任意一点,点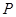 在射线
在射线 上,且满足
上,且满足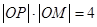 ,记点
,记点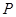 的轨迹为
的轨迹为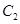 .
.
(1)求曲线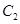 的极坐标方程;
的极坐标方程;
(2)求曲线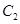 上的点到直线
上的点到直线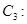
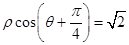 的距离的最大值.
的距离的最大值.