“校园手机”现象越来越受到社会的关注,小记者刘红随机调查了某校若干学生和家长对中学生带手机现象的看法,制作了如下的统计图: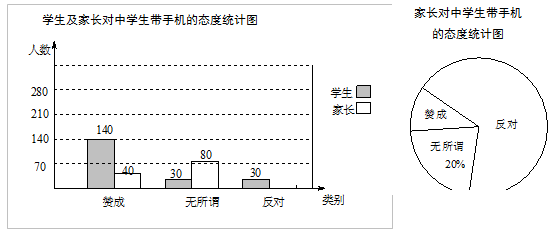
(1)求这次调查的总人数,并补全图1;
(2)求图2中表示家长“赞成”的圆心角的度数;
(3)针对随机调查的情况,刘红决定从初三一班表示赞成的4位家长中随机选择2位进行深入调查,其中包含小亮和小丁的家长,请你利用树状图或列表的方法,求出小亮和小丁的家长被同时选中的概率.
如图,⊙O是△ACD的外接圆,AB是直径,过点D作直线DE∥AB,过点B作直线BE∥AD,两直线交于点E,如果∠ACD=45°,⊙O的半径是4cm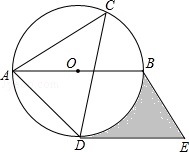
(1)请判断DE与⊙O的位置关系,并说明理由;
(2)求图中阴影部分的面积(结果用π表示).
某校对九年级全体学生进行了一次学业水平测试,成绩评定分为A,B,C,D四个等级(A,B,C,D分别代表优秀、良好、合格、不合格)该校从九年级学生中随机抽取了一部分学生的成绩,绘制成以下不完整的统计图.请你根据统计图提供的信息解答下列问题;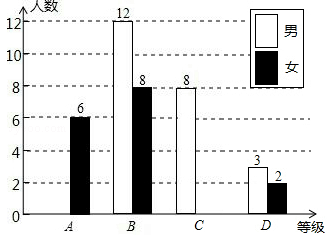
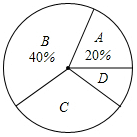
(1)本次调查中,一共抽取了 名学生的成绩;
(2)将上面的条形统计图补充完整,写出扇形统计图中等级C的百分比 .
(3)若等级D的5名学生的成绩(单位:分)分别是55、48、57、51、55.则这5个数据的中位数是 分,众数是 分.
(4)如果该校九年级共有500名学生,试估计在这次测试中成绩达到优秀的人数.
(1)计算: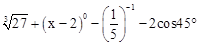
(2)先化简,再求值: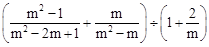 ,其中m=﹣3.
,其中m=﹣3.
如图,正方形AOCB在平面直角坐标系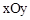 中,点O为原点,点B在反比例函数
中,点O为原点,点B在反比例函数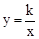 (
(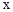 >
>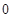 )图象上,△BOC的面积为
)图象上,△BOC的面积为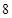 .
.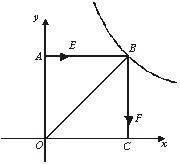
(1)求反比例函数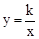 的关系式;
的关系式;
(2)若动点E从A开始沿AB向B以每秒1个单位的速度运动,同时动点F 从B开始沿BC向C以每秒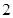 个单位的速度运动,当其中一个动点到达端点时,另一个动点随之停止运动.若运动时间用t表示,△BEF的面积用
个单位的速度运动,当其中一个动点到达端点时,另一个动点随之停止运动.若运动时间用t表示,△BEF的面积用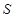 表示,求出S关于t的函数关系式,并求出当运动时间t取何值时,△BEF的面积最大?
表示,求出S关于t的函数关系式,并求出当运动时间t取何值时,△BEF的面积最大?
(3)当运动时间为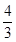 秒时,在坐标轴上是否存在点P,使△PEF的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
秒时,在坐标轴上是否存在点P,使△PEF的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
青海新闻网讯:西宁市为加大向国家环境保护模范城市大步迈进的步伐,积极推进城市绿地、主题公园、休闲场地建设.园林局利用甲种花卉和乙种花卉搭配成A、B两种园艺造型摆放在夏都大道两侧.搭配数量如下表所示:
| 甲种花卉(盆) |
乙种花卉(盆) |
|
| A种园艺造型(个) |
 盆 盆 |
 盆 盆 |
| B种园艺造型(个) |
 盆 盆 |
 盆 盆 |
(1)已知搭配一个A种园艺造型和一个B种园艺造型共需 元.若园林局搭配A种园艺造型
元.若园林局搭配A种园艺造型 个,B种园艺造型
个,B种园艺造型 个共投入
个共投入 元.则A、B两种园艺 造型的单价分别是多少元?
元.则A、B两种园艺 造型的单价分别是多少元?
(2)如果搭配A、B两种园艺造型共 个,某校学生课外小组承接了搭配方案的设计,其中甲种花卉不超过
个,某校学生课外小组承接了搭配方案的设计,其中甲种花卉不超过 盆,乙种花卉不超过
盆,乙种花卉不超过 盆,问符合题意的搭配方案有几种?请你帮忙设计出来.
盆,问符合题意的搭配方案有几种?请你帮忙设计出来.