在直角坐标系
中，已知点P是反比例函数
（
＞0）图象上一个动点，以P为圆心的圆始终与
轴相切，设切点为A．
（1）如图1，⊙P运动到与轴相切，设切点为K，试判断四边形OKPA的形状，并说明理由．
（2）如图2，⊙P运动到与轴相交，设交点为B，C．当四边形ABCP是菱形时：
①求出点A，B，C的坐标．
②在过A，B，C三点的抛物线上是否存在点M，使△MBP的面积是菱形ABCP面积的
．若存在，试求出所有满足条件的M点的坐标，若不存在，试说明理由．
如图1，四边形ABCD中，AD∥BC，∠A=90°，BD⊥CD，AD=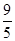
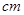，BC=5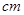，动点P从点D出发，以1cm/s的速度沿DB方向运动，动点Q也从点D出发，以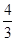
/
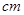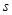的速度沿DC方向运动，P，Q两点同时出发，当点Q到达点C时停止运动，点P也随之停止，设运动时间为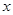
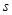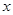（＞0）．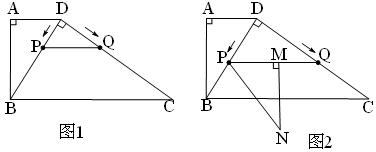
（1）求线段DB的长；
（2）请判断PQ与BC的位置关系，并加以证明；
（3）伴随P，Q两点的运动，将△DPQ绕点P旋转，得到△PMN，点M落在线段PQ上，若△PMN
与△DBC的重叠部分的图形周长为y，
①请求出y与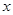之间的函数关系式，并指出自变量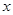的取值范围；
②求出当4＜y≤5时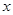的取值范围．
如图，矩形ABCD中，AB=6，BC=10，点P在边BC上，点Q在边CD上，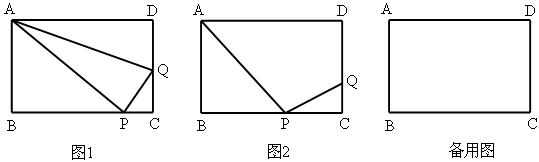
（1）如图1，将△ADQ沿AQ折叠，点D恰好与点P重合，求CQ的长；
（2）如图2，若CQ=2，且△ABP与△PCQ相似，求BP的长；
（3）若点Q是CD边上的一点，且BC上不存在满足AP⊥PQ的点P，请探究：此时CQ的长必须满足什么条件？
某兴趣小组开展课外活动．如图，小明从点M出发以1．5米／秒的速度，沿射线MN方向匀速前进，2秒后到达点B，此时他（AB）在某一灯光下的影长为MB，继续按原速行走2秒到达点D，此时他（CD）在同一灯光下的影子GD仍落在其身后，并测得这个影长GD为1．2米，然后他将速度提高到原来的1．5倍，再行走2秒到达点F，此时点A，C，E三点共线．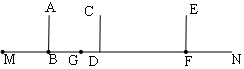
（1）请在图中画出光源O点的位置，并画出小明位于点F时在这个灯光下的影长FH（不写画法）；
（2）求小明到达点F时的影长FH的长．
己知：如图，在菱形ABCD中，点M、N分别在边AD、AB，∠DCM=∠BCN，CN与BD交于点E．
（1）求证：DM=BN；
（2）当四边形MNBE是平行四边形时，求证：
．
在平面直角坐标系中，△ABC的三个顶点坐标分别为A（2，﹣4），B（3，﹣2），C（6，﹣3）．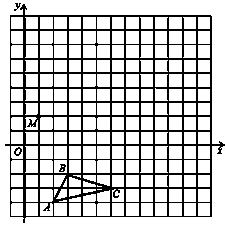
（1）画出△ABC关于x轴对称的△A1B1C1；
（2）以M点为位似中心，在网格中画出△A1B1C1的位似图形△A2B2C2，使△A2B2C2与△A1B1C1的相似比为2∶1．
（3）请写出（2）中放大后的△A2B2C2中A2B2边的中点P的坐标．．