2015年3月2日云南临沧沧源发生
级地震，牵动着全国人民的心，地震后某中学举行了爱心捐款活动，下图是该校九年级某班学生为沧源灾区捐款情况绘制的不完整的条形统计图和扇形统计图．
（1）求该班人数；
（2）补全条形统计图；
（3）在扇形统计图中，捐款“
元人数”所在扇形的圆心角的度数；
（4）若该校九年级有
人，据此样本，请你估计该校九年级学生共捐款多少元？
设二次函数
的图象为C1．二次函数
的图象与C1关于y轴对称．
（1）求二次函数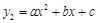
的解析式；
（2）当
≤0时，直接写出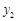
的取值范围；
（3）设二次函数图象的顶点为点A，与y轴的交点为点B，一次函数
（ k，m为常数，k≠0）的图象经过A，B两点，当
时，直接写出x的取值范围．
已知二次函数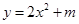
．
（1）若点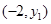
与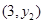
在此二次函数的图象上，则
（填 “>”、“=”或“<”）；
（2）如图，此二次函数的图象经过点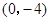
，正方形ABCD的顶点C、D在x轴上， A、B恰好在二次函数的图象上，求图中阴影部分的面积之和．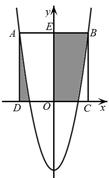
如图，AB为⊙O的直径，射线AP交⊙O于C点，∠PCO的平分线交⊙O于D点，过点D作
交AP于E点．
（1）求证：DE为⊙O的切线；
（2）若DE=3，AC=8，求直径AB的长．
如图，用长为20米的篱笆恰好围成一个扇形花坛，且扇形花坛的圆心角小于180°，设扇形花坛的半径为r米，面积为S平方米．（注：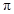
的近似值取3）
（1）求出S与r的函数关系式，并写出自变量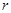
的取值范围；
（2）当半径r为何值时，扇形花坛的面积最大，并求面积的最大值．
如图，AB是⊙O的弦，OC⊥AB于点C，连接OA，AB=12，⊙O半径为10．
（1）求OC的长；
（2）点E，F在⊙O上，EF∥AB．若EF=16，直接写出EF与AB之间的距离．