如图甲所示,不变形、足够长、质量为m1=0.2kg的“U”形金属导轨PQMN放在绝缘水平桌面上,QP与MN平行且距离d=1m,Q、M间导体电阻阻值R=4Ω,右内侧紧靠两固定绝缘小立柱1、2;光滑金属杆KL电阻阻值r=1Ω,质量m2=0.1kg,垂直于QP和MN,与QM平行且距离L=0.5m,左侧紧靠两固定绝缘小立柱3、4。金属导轨与桌面的动摩擦因数μ=0.5,最大静摩擦力等于滑动摩擦力,其余电阻不计。从t=0开始,垂直于导轨平面的磁场磁感应强度如图乙所示。
(1)求在整个过程中,导轨受到的静摩擦力的最大值fmax;
(2)如果从t=2s开始,给金属杆KL水平向右的外力,外力对金属杆作用的功率保持不变为P0=320W,杆到达最大速度时撤去外力,求撤去外力后QM上产生的热量QR=?
跳伞运动员做低空跳伞表演,他在离地面224m高处,由静止开始在竖直方向做自由落体运动一段时间后,立即打开降落伞,以12.5m/s2的平均加速度匀加速下降,为了运动员的安全,要求运动员落地速度最大不得超过5m/s(g取10 m/s2)
(1)运动员着地时相当于从多高处自由落下?
(2)运动员展开伞时,离地面高度至少为多少?
我国首个月球探测计划“嫦娥工程”将分三个阶段实施,大约用十年的时间完成,这极大地提高了同学们对月球的关注,以下是某位同学就有关月球的知识设计的两个问题,请你回答:
(1)若已知地球的半径为R,地球表面的重力加速度为g,月球绕地球运行的周期为T,且把月球绕地球的运行近似看作是匀速圆周运动。试求出月球绕地球运行的轨道半径.
(2)若某位宇航员随登月飞船登陆月球后,在月球某水平表面上方h高处以速度 水平抛出一个小球,小球落回月球表面时与抛出点间的水平距离为s,已知月球的半径为
水平抛出一个小球,小球落回月球表面时与抛出点间的水平距离为s,已知月球的半径为 ,引力常量为G,试求月球的质量
,引力常量为G,试求月球的质量 .
.
一根长度为L的轻质直杆两端各固定一个可视为质点的小球A和B,两小球质量均为m,直杆可以绕过其中点O的水平轴在竖直平面内匀速转动,若直杆匀速转动周期为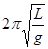 ,求
,求
(1)小球转动的角速度;
(2)直杆转动到如图竖直位置时,A、B两小球对直杆作用力各多大?方向如何?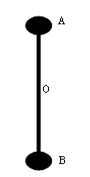
一辆汽车在平直公路上做匀变速直线运动,公路边每隔15m有一棵树,如图所示,汽车通过AB两相邻的树用了3s,通过BC两相邻的树用了2s,求汽车运动的加速度和通过树B时的速度为多少?
一架飞机着陆时的速度大小为60m/s,着陆后以6m/s2大小的加速度做匀减速直线运动,求:
(1)它着陆后滑行225m时的速度大小;
(2)它着陆后12s内滑行的位移大小。