已知,点P是∠MON的平分线上的一动点,射线PA交射线OM于点A,将射线PA绕点P逆时针旋转交射线ON于点B,且使∠APB+∠MON=180°.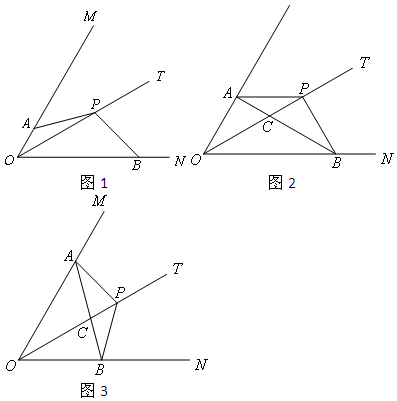
(1)利用图1,求证:PA=PB;
(2)如图2,若点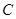 是
是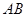 与
与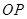 的交点,当
的交点,当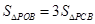 时,求PB与PC的比值;
时,求PB与PC的比值;
(3)若∠MON=60°,OB=2,射线AP交ON于点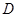 ,且满足且
,且满足且 ,请借助图3补全图形,并求
,请借助图3补全图形,并求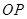 的长.
的长.
如图(1),点A、B、C在同一直线上,且△ABE, △BCD都是等边三角形,连结AD,CE.△BEC可由△ABD顺时针旋转得到吗?若是,请描述这一旋转变换过程;若不是,请说明理由;
若△BCD绕点B顺时针旋转,使点A,B,C不在同一直线上(如图(2)),则在旋转过程中:
①线段AD与EC的长度相等吗?请说明理由.
②锐角 的度数是否改变?若不变,请求出
的度数是否改变?若不变,请求出 的度数;若改变,请说明理由.
的度数;若改变,请说明理由.
(注:等边三角形的三条边都相等,三个内角都是60°)

如图,有牌面数字都是2,3,4的两组牌.从每组牌中各随机摸出一张,请用画树状图或列表的方法,求摸出的两张牌的牌面数字之和为6的概率. 
如图,在正方形的网格图(每小格边长均为1的正方形)中,完成下列各题: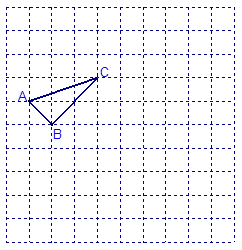
将⊿ABC向右平移4个单位得到⊿A1B1C1;
画出⊿A1B1C1绕点C1逆时针旋转90º所得的⊿A2B2C1;
把⊿ABC的每条边扩大到原来的2倍得到⊿A3B3C3;(顶点画在网格点上).
如图,AC=AD,∠BAC=∠BAD,点E在AB上.
.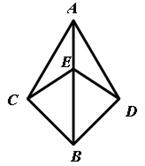
你能找出 对全等的三角形
请写出一对全等三角形,并说明理由
在下列三个二元一次方程中,请你选择合适的两个方程组成二元一次方程组,然后求出方程组的解.可供选择的方程:① y=2x-3② 2x+y=5③ 4x-y=7.