（贵州遵义）如图，一楼房AB后有一假山，其坡度
，山坡坡面上E点处有一休息亭，测得假山坡脚C与楼房水平距离BC＝25米，与亭子距离CE＝20米．小丽从楼房顶测得E点的俯角为45°，求楼房AB的高．（注：坡度i是指坡面的铅直高度与水平宽度的比）
已知：如图，点A、F、C、D在同一直线上，点B和点E分别在直线AD的两侧，且AB=DE，∠A=∠D，AF=DC．求证：△ABC≌△DEF．
有这样的一个定理：夹在两条平行线间的平行线段相等．下面经历探索与应用的过程．
探索：
已知：如图1，AD∥BC，AB∥CD．求证：AB=CD．
应用此定理进行证明求解．
应用一、已知：如图2，AD∥BC，AD＜BC，AB=CD．求证：∠B=∠C；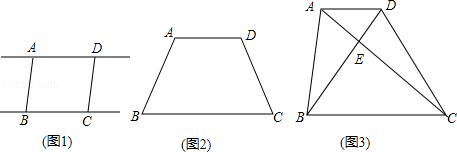
应用二、已知：如图3，AD∥BC，AC⊥BD，AC=4，BD=3．求：AD与BC两条线段的和．
如图1，四边形OABC中，OA=a，OC=3，BC=2，∠AOC=∠BCO=90°，经过点O的直线l将四边形分成两部分，直线l与
OC所成的角设为θ，将四边形OABC的直角∠OCB沿直线l折叠，点C落在点D处（如图1）．
（1）若折叠后点D恰为AB的中点（如图2），则θ= ；
（2）若θ=45°，四边形OABC的直角∠OCB沿直线l折叠后，点B落在点四边形OABC的边AB上的E处（如图3），求a的值．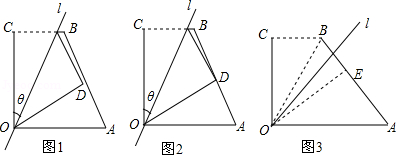
如图，在△ABC中，AB=17，BC=16，BC边上的中线AD=15，
（1）求AC；
（2）若点P在边AC上移动，则BP的最小值是 ．
如图，一个梯子AB长2．5米，顶端A靠在墙AC上，这时梯子下端B与墙角C距离为0．7米，梯子滑动后停在DE的位置上，测得BD长为1．3米，求梯子顶端A下落了多少米？