为邓小平诞辰110周年献礼，广安市政府对城市建设进行了整改．如图，已知斜坡AB长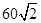
米，坡角（即∠BAC）为45°，BC⊥AC，现计划在斜坡中点D处挖去部分斜坡，修建一个平行于水平线CA的休闲平台DE和一条新的斜坡BE（下面两个小题结果都保留根号）．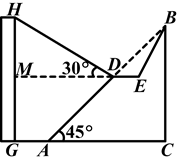
（1）若修建的斜坡BE的坡比为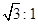
，求休闲平台DE的长是多少米；
（2）一座建筑物GH距离A点33米远（即AG＝33米），小亮在D点测得建筑物顶部H的仰角（即∠HDM）为30°．点B、C、A、G、H在同一个平面内，点C、A、G在同一条直线上，且HG⊥CG，问建筑物GH高为多少米？
某区教研部门对本区初二年级的学生进行了一次随机抽样问卷调查，其中有这样一个问题：
老师在课堂上放手让学生提问和表达 （）
A 从不；B 很少；C 有时；D 常常；E 总是
答题的学生在这五个选项中只能选择一项．下面是根据学生对该问题的答卷情况绘制的两幅不完整的统计图．
根据以上信息，解答下列问题：
（1）该区共有名初二年级的学生参加了本次问卷调查；
（2）请把这幅条形统计图补充完整；
（3）在扇形统计图中，“总是”所占的百分比为．
已知：如图，AB为⊙O的直径，点C、D在⊙O上，且BC＝6cm，AC＝8cm，∠ABD＝45º．
（1）求BD的长；
（2）求图中阴影部分的面积．
已知：如图，AB∥CD，E是AB的中点，CE＝DE．
求证：（1）∠AEC＝∠BED；
（2）AC＝BD．
（1）解不等式：2（x－3）－2≤0；
（2）解方程组：
计算：
（1）（－5）0－（
）2＋|－3|；
（2）（x＋1）2－2（x－2）．