如图在△ABC中,BE平分∠ABC,∠C=90°,D在AB边上,以DB为直径的半圆O经过点E交BC于点F.
(1)求证:AC是⊙O的切线;
(2)已知sinA= ,⊙O的半径为4,求图中阴影部分的面积.
,⊙O的半径为4,求图中阴影部分的面积.
(1)计算: ;
(2)先化简,再求值: ,其中 , .
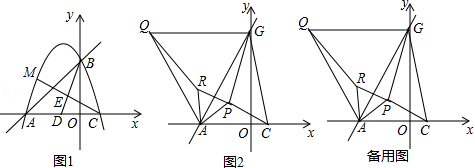
如图1,已知一次函数 的图象与 轴、 轴分别交于 、 两点,抛物线 过 、 两点,且与 轴交于另一点 .
(1)求 、 的值;
(2)如图1,点 为 的中点,点 在线段 上,且 ,连接 并延长交抛物线于点 ,求点 的坐标;
(3)将直线 绕点 按逆时针方向旋转 后交 轴于点 ,连接 ,如图2, 为 内一点,连接 、 、 ,分别以 、 为边,在他们的左侧作等边 ,等边 ,连接
①求证: ;
②求 的最小值,并求出当 取得最小值时点 的坐标.
如图,在四边形 中, , , ,以点 为圆心, 为半径的圆与 相切于点 ,交 于点
(1)求 的大小及 的长度;
(2)在 的延长线上取一点 ,使得 上的一个动点 到点 的最短距离为 ,求 的长.

我市某蔬菜生产基地用装有恒温系统的大棚栽培一种适宜生长温度为 的新品种,如图是某天恒温系统从开启到关闭及关闭后,大棚里温度 随时间 变化的函数图象,其中 段是恒温阶段, 段是双曲线 的一部分,请根据图中信息解答下列问题:
(1)求 的值;
(2)恒温系统在一天内保持大棚里温度在 及 以上的时间有多少小时?

一个不透明的袋子中装有大小、质地完全相同的4只小球,小球上分别标有1、2、3、4四个数字
(1)从袋中随机摸出一只小球,求小球上所标数字为奇数的概率;
(2)从袋中随机摸出一只小球,再从剩下的小球中随机摸出一只小球,求两次摸出的小球上所标数字之和为5的概率.