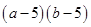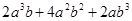（本小题满分8分）有两把不同的锁和四把不同的钥匙，其中两把钥匙恰好分别能打开这两把锁，其余的钥匙不能打开这两把锁．现在任意取出一把钥匙去开任意一把锁．请用列表或画树状图的方法求一次打开锁的概率．
如图，在Rt△ABC中，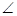
C=90°，AC=4，BC=3，以△ABC的一边为边作等腰三角形，使它的第三个顶点在△ABC的其他边上.请在图①、图②、图③中分别画出一个符合条件得等腰三角形，且三个图形中的等腰三角形各不相同，并在图中标明所画等腰三角形的腰长（不要求尺规作图）. 
如图，已知在△ABC中，∠1＝∠2.
请你添加一个与直线AC有关的条件，由此可得出BE是△ABC的外角平分线；
请你添加一个与∠1有关的条件，由此可得出BE是△ABE的外角平分线；
如果“已知在△ABC中，∠1＝∠2不变”，请你把（1）中添加的条件与所得结论互换，还正确吗?理由是什么？
有足够多的长方形和正方形的卡片，如下图. 
如果选取1号、2号、3号卡片分别为1张、2张、3张，可拼成一个长方形（不重叠无缝隙）.请画出这个长方形的草图，并运用拼图前后面积之间的关系说明这个长方形的代数意义.
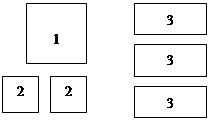
这个长方形的代数意义是.小明如果要拼一个长为（a+2b），宽为（a+3b）的长方形，那么需用2号卡片张，3号卡片张
已知方程组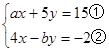
，由于甲看错了方程①中的a，得到方程组的解为x= -3，y=-1；乙看错了方程②中的b，得到方程组的解为x= 5，y=4，若按正确的a，b计算，求原方程组的解x与y的差
已知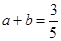
，
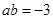求下列代数式的值：
