（本小题5分）如图，在图中求作⊙P，使⊙P满足以线段MN为弦，且圆心P到∠AOB两边的距离相等（要求：尺规作图，不写作法，保留作图痕迹，并把作图痕迹用黑色签字笔加黑）。
如图，四边形ABCD中，AB = AD，∠BAD=90°，∠CBD=30°，∠BCD=45°，
若AB=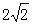
.求四边形
的面积．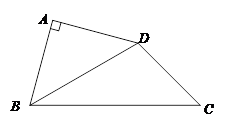
列方程或方程组解应用题：
去年暑期，某地由于暴雨导致电路中断，该地供电局组织电工进行抢修．供电局距离抢修工地15千米．抢修车装载着所需材料先从供电局出发，10分钟后，电工乘吉普车从同一地点出发，结果他们同时到达抢修工地．已知吉普车速度是抢修车速度的1.5倍，求吉普车的速度．
如图，在平面直角坐标系xOy中，直线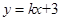
的图象与反比例函数
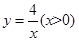的图象交于点A(1，m)，与x轴交于点
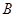，过点A作
轴于点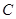
．
（1）求一次函数的解析式；
（2）若P为x轴上一点，且△ABP的面积为10，直接写出点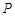
的坐标．
已知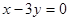
,求代数式
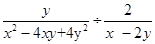的值．
已知：如图，在△ABC中，AD是中线，分别过点B、C作AD及其延长线的垂线BE、CF，垂足分别为点E、F．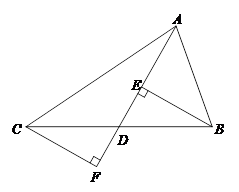
求证：BE=CF．