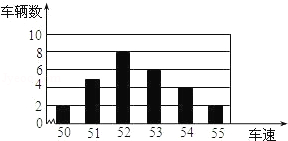
如图,在平面直角坐标系中,抛物线经过点
,其对称轴与
轴交于点
.

(1)求此抛物线的解析式和对称轴;
(2)在此抛物线的对称轴上是否存在一点
,使
的周长最小?若存在,请求出点
的坐标;若不存在,请说明理由;
(3)连接AC,在直线
下方的抛物线上,是否存在一点
,使
的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.
如图,抛物线y=ax2+bx+c(a<0)与双曲线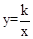 相交于点A,B,且抛物线经过坐标原点,点A的坐标为(﹣2,2),点B在第四象限内,过点B作直线BC∥x轴,点C为直线BC与抛物线的另一交点,已知直线BC与x轴之间的距离是点B到y轴的距离的4倍,记抛物线顶点为E.
相交于点A,B,且抛物线经过坐标原点,点A的坐标为(﹣2,2),点B在第四象限内,过点B作直线BC∥x轴,点C为直线BC与抛物线的另一交点,已知直线BC与x轴之间的距离是点B到y轴的距离的4倍,记抛物线顶点为E.
(1)求双曲线和抛物线的解析式;
(2)计算△ABC与△ABE的面积;
(3)在抛物线上是否存在点D,使△ABD的面积等于△ABE的面积的8倍?若存在,请求出点D的坐标;若不存在,请说明理由.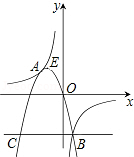
如图,已知AB为⊙O的直径,PA与⊙O相切于点A,线段OP与弦AC垂直并相交于点D,OP与弧AC相交于点E,连接BC.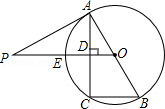
(1)求证:∠PAC=∠B,且PA•BC=AB•CD;
(2)若PA=10,sinP=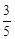 ,求PE的长.
,求PE的长.
如图,某化工厂与A,B两地有公路和铁路相连,这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运到B地.已知公路运价为1.5元/(吨•千米),铁路运价为1.2元/(吨•千米),这两次运输共支出公路运费15 000元,铁路运费97 200元,请计算这批产品的销售款比原料费和运输费的和多多少元?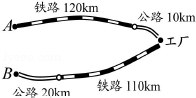
(1)根据题意,甲、乙两名同学分别列出尚不完整的方程组如下:
甲: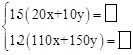
乙:
根据甲,乙两名同学所列方程组,请你分别指出未知数x,y表示的意义,然后在等式右边的方框内补全甲、乙两名同学所列方程组.
甲:x表示 ▲ ,y表示 ▲
乙:x表示 ▲ ,y表示 ▲
(2)甲同学根据他所列方程组解得x=300,请你帮他解出y的值,并解决该实际问题.
如图,线段AB,DC分别表示甲、乙两建筑物的高.某初三课外兴趣活动小组为了测量两建筑物的高,用自制测角仪在B外测得D点的仰角为α,在A处测得D点的仰角为β.已知甲、乙两建筑物之间的距离BC为m.请你通过计算用含α、β、m的式子分别表示出甲、乙两建筑物的高度.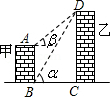
如图是交警在一个路口统计的某个时段来往车辆的车速情况(单位:千米/时)
(1)找出该样本数据的众数和中位数;
(2)计算这些车的平均速度;(结果精确到0.1)
(3)若某车以50.5千米/时的速度经过该路口,能否说该车的速度要比一半以上车的速度快?并说明判断理由.