如图,在▱ABCD中,对角线AC与BD相交于点O,∠CAB=∠ACB,过点B作BE⊥AB交AC于点E.
(1)求证:AC⊥BD;
(2)若AB=14,cos∠CAB=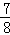 ,求线段OE的长.
,求线段OE的长.
已知:如图,在△ABC中,A(a,0),B(b,0),C(0,c),且a、b、c满足
b=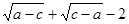 ,BD⊥AC于D,交y轴于E.
,BD⊥AC于D,交y轴于E.

(1)如图1,求E点的坐标;
(2)如图2,过A点作AG⊥BC于G,若∠BCO=30°,求证:AG+GC=CB+BO.
(3)如图3,P为第一象限任意一点,连接PA,作PQ⊥PA交y轴于Q点,在射线PQ上截取PH="PA," 连接CH, F为CH的中点,连接OP,当P点运动时(PQ不过点C), ∠OPF的大小是否发生变化,若不变,求其度数,若变化,求其变化范围.
在▱ABCD中,∠ADC的平分线交直线BC于点E、交AB的延长线于点F,连接AC.
(1)如图1,若∠ADC=90°,G是EF的中点,连接AG、CG.
①求证:BE=BF.
②请判断△AGC的形状,并说明理由;
(2)如图2,若∠ADC=60°,将线段FB绕点F顺时针旋转60°至FG,连接AG、CG.那么△AGC又是怎样的形状.(直接写出结论不必证明)
如图,在矩形ABCD中,E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G.
(1)猜想线段GF与GC有何数量关系?并证明你的结论;
(2)若AB=3,AD=4,求线段GC的长;
水池中有水,水面是一个边长为10尺的正方形,水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面.水的深度和这根芦苇的长度分别是多少?
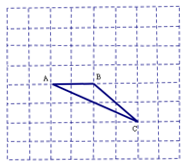
如图在8×8的正方形网格中,△ABC的顶点在边长为1的小正方形的顶点上。填空:∠ABC =,BC =若点A在网格所在的坐标平面里的坐标为(1,-2),请你在图中找出一点并作出以A、B、C、D四个点为顶点的平行四边形,求出满足条件的D点的坐标。