如图,正方形ABCD的边长为8cm,E、F、G、H分别是AB、BC、CD、DA 上的动点,且AE=BF=CG=DH.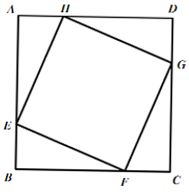
(1)求证:四边形EFGH是正方形;
(2)判断直线EG是否经过一个定点,并说明理由;
(3)求四边形EFGH面积的最小值。
先化简,再求值 3x2y﹣[2xy﹣2(xy﹣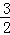 x2y)+xy],其中x=3,y=﹣
x2y)+xy],其中x=3,y=﹣ .
.
解不等式组 .
.
解不等式2(x+1)﹣1≥4x+3,并把它的解集在数轴上表示出来.
解方程:
(1)5x﹣1=3(x+1)
(2)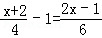 .
.
有一种“二十四点”的游戏,其游戏规则是这样的:任取四个1至13之间的自然数,将这四个数(每个数用且只用一次)进行加减乘除四则运算,使其结果等于24.例如对1,2,3,4可作运算:(1+2+3)×4=24.[注意上述运算与4×(2+3+1)应视为相同方法的运算].现有四个有理数3,4,﹣6,10,运用上述规则写出三种不同方法的运算式,使其结果等于24,运算式如下:
(1) ;
(2) ;
(3) .