已知点 F 是抛物线 y 2 = 4x的焦点，M、N 是该抛物线上两点，| MF | + | NF | = 6，则 MN中点的横坐标为（ ）
A． |
B．2 | C． |
D．3 |
函数y=2x3-3x2-12x+5在区间[0,3]上最大值与最小值分别是 ( ▲ )
.
| A．5,-15 | B．5,-4 | C．-4,-15 | D．5,-16 |
已知复数z＝1－2i，那么等于( ▲ )
| A．＋i | B．－i | C．＋i | D．－i |
设f(x)为可导函数，且满足条件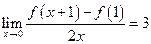
，则曲线
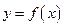在点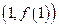
处的切线的斜率为( ▲ )
| A． | B．3 | C．6 | D．无法确定 |
过双曲线
的右顶点A作斜率为-1的直线,该直线与双曲线的两条渐近线的交点分别为B,C.若
,则双曲线的离心率是（ ）
(A)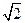
(B)
(C)
(D)
设P为曲线C：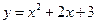
上的点，且曲线C在点P处切线倾斜角的取值范围为
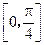，则点P横坐标的取值范围为（ ）
A． |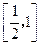
B． |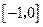
C． |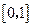
D． |