下图是正态分布N(0,1)的正态曲线图,下面3个式子中,等于图中阴影部分面积的个数为()。注:Φ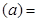 P
P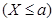
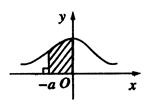
①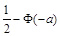 ②
②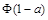 ③
③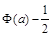
| A.0 | B.1 | C.2 | D.3 |
编号为1、2、3、4的四个人入座编号为1、2、3、4的四个座位,则其中至少有两个人的编号与座位号相同的概率是()
A.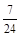 |
B.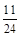 |
C.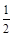 |
D.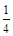 |
对两个变量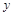 和
和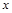 进行回归分析,得到一组样本数据:
进行回归分析,得到一组样本数据: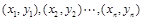 ,则下列说法中不正确的是()
,则下列说法中不正确的是()
A.由样本数据得到的回归方程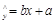 必过样本中心 必过样本中心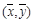 |
| B.残差平方和越小的模型,拟合的效果越好 |
C.用相关指数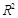 来刻画回归效果, 来刻画回归效果,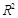 越小,说明模型的似合效果越好 越小,说明模型的似合效果越好 |
D.若变量y和x之间的相关系数为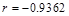 ,则变量y和x之间具有线性相关关系 ,则变量y和x之间具有线性相关关系 |
掷两颗骰子,所得点数之和为 ,那么
,那么 =4表示的随机试验结果是()
=4表示的随机试验结果是()
| A.一颗是3点,一颗是1点 | B.两颗都是2点 |
| C.两颗都是4点 | D.一颗是3点,一颗是1点或两颗都是2点 |
已知函数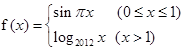 ,若
,若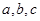 互不相等,且
互不相等,且 ,则
,则 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |