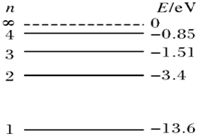
在图甲所示的装置中,K为一金属板,A为金属电极,都密封在真空的玻璃管中,W为由石英片封盖的窗口,单色光可通过石英片射到金属板K上,E为输出电压可调的直流电流,其负极与电极A相连,A是电流表,实验发现,当用某种频率的单色光照射K时,K会发出电子(光电效应),这时,即使A、K之间的电压等于零,回路中也有电流.当A的电势低于K时,而且当A比K的电势低到某一值Uc时,电流消失,Uc称为遏止电压,当改变照射光的频率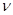 ,遏止电压Uc也将随之改变,其关系如图乙所示,如果某次实验我们测出了画出这条图线所需的一系列数据,又知道了电子电量,则( )
,遏止电压Uc也将随之改变,其关系如图乙所示,如果某次实验我们测出了画出这条图线所需的一系列数据,又知道了电子电量,则( )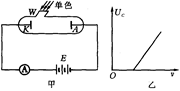
A.可得该金属的极限频率 B.可求得该金属的逸出功
C.可求得普朗克常量 D.可求得电子的质量
地球同步卫星到地心的距离r可由 求出.已知式中a的单位是m,b的单位是s,c的单位是m/s2,则()
求出.已知式中a的单位是m,b的单位是s,c的单位是m/s2,则()
| A.a是地球半径,b是地球自转的周期,c是地球表面处的重力加速度 |
| B.a是地球半径,b是同步卫星绕地心运动的周期,c是同步卫星的加速度 |
| C.a是赤道周长,b是地球自转的周期,c是同步卫星的加速度 |
| D.a是地球半径,b是同步卫星绕地心运动的周期,c是地球表面处的重力加速度 |
关于开普勒行星运动的公式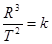 ,以下理解正确的是()
,以下理解正确的是()
| A.k是一个与行星无关的常量 | |
| B.若地球绕太阳运转轨道的半长轴为R地,周期为T地;月球绕地球运转轨道的长半轴为 R月,周期为T月,则 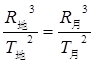 |
|
| C.T表示行星运动的自转周期 | D.T表示行星运动的公转周期 |
一宇宙飞船绕地球做匀速圆周运动,飞船原来的线速度是v1,周期是T1,假设在某时刻它向后喷气做加速运动后,进入新轨道做匀速圆周运动,运动的线速度是v2,周期是T2,则:
| A.v1>v2,T1>T2 | B.v1>v2,T1<T2 |
| C.v1<v2,T1>T2 | D.v1<v2,T1<T2 |
质量为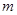 的物体始终固定在倾角为
的物体始终固定在倾角为 的斜面上,下列说法正确的是()
的斜面上,下列说法正确的是()
A.若斜面水平向右匀速运动距离为 ,斜面对物体不做功。 ,斜面对物体不做功。 |
B.若斜面竖直向上匀速运动距离为 ,斜面对物体不做功。 ,斜面对物体不做功。 |
C.若斜面水平向左以加速度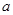 运动距离 运动距离 ,斜面对物体做功 ,斜面对物体做功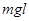 |
D.若斜面竖直向下以加速度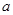 运动距离 运动距离 ,斜面对物体做功 ,斜面对物体做功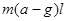 |
若已知行星绕太阳公转的半径为r,公转的周期为T,万有引力恒量为G,则由此可求出()
| A.某行星的质量 | B.太阳的质量 | C.某行星的密度 | D.太阳的密度 |