设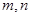 为两条不同的直线,
为两条不同的直线,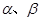 为两个不同的平面.下列命题中,正确的是( )
为两个不同的平面.下列命题中,正确的是( )
A.若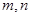 与 与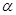 所成的角相等,则 所成的角相等,则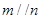 |
B.若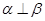 , ,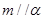 ,则 ,则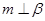 |
C.若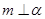 , ,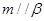 ,则 ,则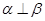 |
D.若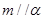 , , ,则 ,则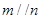 |
已知函数f(x)=x2+(2a﹣1)x+b是偶函数,那么函数 的定义域为()
的定义域为()
A. |
B. |
| C.(0,2] |
| D.[2,+∞) |
函数y=2x﹣x2的图象大致是()
A. |
B. |
C. |
D. |
函数y=f(x)在[0,2]上单调递增,且函数f(x+2)是偶函数,则下列结论成立的是()
A.f(1)<f(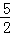 )<f( )<f(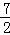 ) ) |
B.f(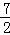 )<f(1)<f( )<f(1)<f(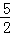 ) ) |
C.f(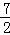 )<f( )<f(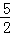 )<f(1) )<f(1) |
D.f(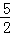 )<f(1)<f( )<f(1)<f(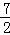 ) ) |
函数f(x)= +
+ 的定义域为()
的定义域为()
| A.[﹣2,+∞) |
| B.(﹣∞,﹣2] |
| C.R |
| D.[﹣2,1)∪(1,+∞) |
设偶函数f(x)满足f(x)=2x﹣4(x≥0),则{x|f(x﹣2)<0}=()
| A.{x|x<﹣2或x>4} |
| B.{x|x<0或x>4} |
| C.{x|x<0或x>6} |
| D.{x|0<x<4} |