如图示,竖直平面内一光滑水平轨道左边与墙壁对接,右边与一足够高的1/4光滑圆弧轨道平滑相连,木块A、 B静置于光滑水平轨道上,A、B质量分别为1.5kg和0.5kg。现让A以6m/s的速度水平向左运动,之后与墙壁碰撞,碰撞时间为0.3s,碰后速度大小变为4m/s。当A与B碰撞后会立即粘在一起运动,已知g=10m/s2 求:
①A与墙壁碰撞过程中,墙壁对小球平均作用力的大小;
②A、B滑上圆弧轨道的最大高度。
质量为M的小物块A静止在离地面高h的水平桌面的边缘,质量为m的小物块B沿桌面向A运动以速度v0与之发生正碰(碰撞时间极短)。碰后A离开桌面,其落地点离出发点的水平距离为L。碰后B反向运动。求B后退的距离。已知B与桌面间的动摩擦因数为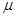 。重力加速度为g。
。重力加速度为g。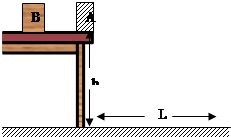
如图所示,长度为l的轻绳上端固定在O点,下端系一质量为m 的小球(小球的大小可以忽略)。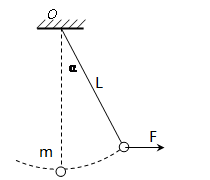
(1)在水平拉力F的作用下,轻绳与竖直方向的夹角为α,小球保持静止。画出此时小球的受力图,并求力F的大小;
(2)由图示位置无初速释放小球,求当小球通过最低点时的速度大小及轻绳对小球的拉力。不计空气阻力。
质量m=2kg的物体静止在水平地面上,用F=18N的水平力拉物体,在开始的2s内物体发生了10m位移,此后撤去力F,求:
⑴ 撤去力F时物体的速度;
⑵ 撤去力F后物体运动的最大位移.
如图,质量 的物体静止于水平地面的A处,A、B间距L=20m。用大小为30N,沿水平方向的外力拉此物体,经
的物体静止于水平地面的A处,A、B间距L=20m。用大小为30N,沿水平方向的外力拉此物体,经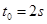 拉至B处。(已知
拉至B处。(已知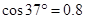 ,
,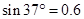 。取
。取 )
)
(1)求物体与地面间的动摩擦因数μ;
(2)用大小为30N,与水平方向成37°的力斜向上拉此物体,使物体从A处由静止开始运动并能到达B处,求该力作用的最短时间t。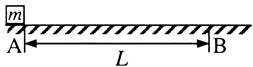
一列货车以28.8km/h的速度在铁路上运行,由于调度事故,在后方700m处有一列快车以72km/h的速度行驶,快车司机发觉后立即合上制动器,但快车要滑行2000m才能停下,试通过计算判断两车是否会相撞。