已知抛物线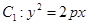 上一点
上一点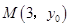 到其焦点
到其焦点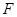 的距离为4;椭圆
的距离为4;椭圆 的离心率
的离心率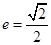 ,且过抛物线的焦点
,且过抛物线的焦点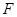 .
.
(1)求抛物线 和椭圆
和椭圆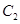 的标准方程;
的标准方程;
(2)过点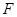 的直线
的直线 交抛物线
交抛物线 于
于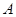 、
、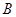 两不同点,交
两不同点,交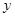 轴于点
轴于点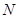 ,已知
,已知 ,求证:
,求证: 为定值.
为定值.
(3)直线 交椭圆
交椭圆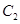 于
于 ,
, 两不同点,
两不同点, ,
, 在
在 轴的射影分别为
轴的射影分别为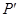 ,
,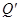 ,
, ,若点S满足:
,若点S满足: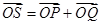 ,证明:点S在椭圆
,证明:点S在椭圆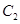 上.
上.
(满分10分)已知复数 满足:
满足: 
(1)求 并求其在复平面上对应的点的坐标;
并求其在复平面上对应的点的坐标;
(2)求 的共轭复数E:\WCFUpload\Upload\2015-08\04\04891303-8df8-452b-8372-8b1d9afe39e5\ http:\\
的共轭复数E:\WCFUpload\Upload\2015-08\04\04891303-8df8-452b-8372-8b1d9afe39e5\ http:\\
(满分10分)(1)用分析法证明:当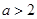 时,
时, ;
;
(2)设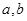 是两个不相等的正数,若
是两个不相等的正数,若 ,用综合法证明:
,用综合法证明:
(本题13分)为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对30名六年级学生进行了问卷调查得到如下列联表:平均每天喝500ml以上为常喝,体重超过50kg为肥胖。
| 常喝 |
不常喝 |
合计 |
|
| 肥胖 |
2 |
||
| 不肥胖 |
18 |
||
| 合计 |
30 |
已知在全部30人中随机抽取1人,抽到肥胖的学生的概率为 。
。
(1)请将上面的列联表补充完整
(2)是否有99.5%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由
(3)现从常喝碳酸饮料且肥胖的学生中(2名女生),抽取2人参加电视节目,则正好抽到一男一女的概率是多少?
参考数据:
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式: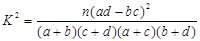 ,其中
,其中 )
)
(本题13分)一家商场为了确定营销策略,进行了投入促销费用x和商场实际销售额y的试验,得到如下四组数据.
| 投入促销费用x(万元) |
2 |
3 |
5 |
6 |
| 商场实际营销额y(万元) |
100 |
200 |
300 |
400 |
(1)在下面的直角坐标系中,画出上述数据的散点图,并据此判断两个变量是否具有较好的线性相关性;
(2)求出x,y之间的回归直线方程 =
= x+
x+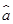 ;
;
(3)若该商场计划营销额不低于600万元,则至少要投入多少万元的促销费用?
(本题10分)已知复数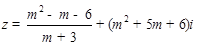
(1)m取什么值时,z是实数?
(2)m 取什么值时,z是纯虚数?