某班开展安全知识竞赛活动,班长将所有同学的成绩分成四类,并制作了如下的统计图表:
根据图表信息,回答下列问题:
(1)该班共有学生 人;表中a= ;
(2)将丁类的五名学生分别记为A、B、C、D、E,现从中随机挑选两名学生参加学校的决赛,请借助树状图、列表或其他方式求B一定能参加决赛的概率.
请根据图中提供的信息,回答下列问题:
(1)一个暖瓶与一个水杯分别是多少元?
(2)甲、乙两家商场同时出售同样的暖瓶和水杯,为了迎接春节,两家商场都在搞促销活动,甲商场规定: 这两种商品都打九折;乙商场规定:买一个暖瓶赠送一个水杯。若某单位想要买4个暖瓶和15个水杯,请问选择哪家商场购买更合算,并说明理由.
元旦期间,弟弟和妈妈从家里出发一同去外婆家,他们走了1小时后,哥哥发现带给外婆的礼品忘在家里,便立刻带上礼品以每小时6千米的速度去追,若弟弟和妈妈每小时行2千米,他们从家里到外婆家需要1小时45分钟,问哥哥能在弟弟和妈妈到外婆家之前追上他们吗?
妈妈为杨杨存了一个6年期的教育储蓄(年期的年利率为2.88﹪),6年后能取5864元,那么刚开始他存入了多少元?
某餐厅中,一张桌子可坐6人,有以下两种摆放方式:
(1)当有n张桌子时,两种摆放方式各能坐多少人?
(2)一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌,若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌?为什么?
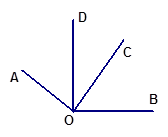
如图,已知AO⊥OC,OB⊥OD,∠AOB =142°,求∠COD的度数。