如图,正比例函数
的图象与反比例函数
的图象交于
、
两点,过点
作
垂直
轴于点
,连结
.若
的面积为
.

(1)求k的值;
(2)x轴上是否存在一点D,使△ABD为直角三角形?若存在,求出点D的坐标;若不存在,请说明理由.
随着生活水平的提高,小林家购置了私家车,这样他乘坐私家车上学比乘 坐公交车上学所需的时间少用了15分钟,现已知小林家距学校8千米,乘私家车平均速度是乘公交车平均速度的2.5倍,问乘公交车平均速度?
在一个不透明的袋子中装有3个除颜色外完全相同的小球,其中白球1个,黄球1个,红球1个,摸出一个球记下颜色后放回,再摸出一个球,请用列表或树形图法求两次都摸到红球的概率.
为了解学生课余活动情况,某校对参加绘画、书法、舞蹈、乐器这四个课外兴趣小组的人员分布情况进行抽样调查,并根据收集的数据绘制了下面两幅不完整的统计图,请根据图中提供的信息,解答下面的问题: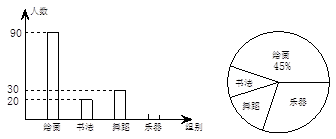
(1)此次共调查了多少名同学?
(2)将条形统计图补充完整,并计算扇形统计图中书法部分的圆心角的度数;
(3)如果该校共有 名学生参加这
名学生参加这 个课外兴趣小组,而每位教师最多只能辅导本组的
个课外兴趣小组,而每位教师最多只能辅导本组的 名学生,估计每个兴趣小组至少需要准备多少名教师.
名学生,估计每个兴趣小组至少需要准备多少名教师.
(1)计算 .(2)解不等式组:
.(2)解不等式组:
【问题情境】
已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
【数学模型】
设该矩形的长为x,周长为y,则y与x的函数关系式为
【探索研究】
(1)我们可以借鉴以前研究函数的经验,先探索函数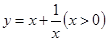 的图象和性质.
的图象和性质.
①填写下表,画出函数的图象;
| x |
… |
 |
 |
 |
1 |
2 |
3 |
4 |
… |
| y |
… |
… |

②观察图象,写出该函数两条不同类型的性质;
③在求二次函数y=ax2+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过配方得到.请你通过配方求函数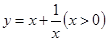 的最小值.
的最小值.
【解决问题】用上述方法解决“问题情境”中的问题,直接写出答案.