如图，为了测量校园水平地面上一棵不可攀的树的高度，学校数学兴趣小组根据光的反射定律，利用一面镜子和一根皮尺，设计如下图所示的测量方案：把一面很小的镜子水平放置在离树底B端8．4米的点E处，然后沿着直线BE后退到点D，这时恰好在镜子里看到树梢顶点A，再用皮尺量得DE=3．2米，观察者目高CD=1．6米，则树AB的高度约为（ ）
| A．4．2米 | B．4．8米 | C．6．4米 | D．16．8米 |
如图，点A在反比例函数y=―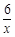
（x＜0）的图象上，点B在反比例函数y=
（x＞0）的图象上，且∠AOB=90°．则tan∠OBA的值等于（）
| A．2 | B．3 | C． |
D． |
已知一次函数
的图象如图所示，则关于x的不等式
的解集为（）
A． |
B． |
C． |
D． |
如图，小红在作线段AB的垂直平分线时，是这样操作的：分别以点A，B为圆心，大于线段AB长度一半的长为半径画弧，相交于点C，D，则直线CD即为所求。连结AC，BC，AD，BD，根据她的作图方法可知，四边形ADBC一定是（）
| A．矩形 | B．菱形 | C．正方形 | D．平行四边形 |
一个正方体的平面展开图如图所示，将它折成正方体后“建”字对面是（）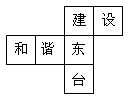
| A．和 | B．谐 | C．东 | D．台 |
如图，一块直角三角板ABC的斜边AB与量角器的直径重合，点D对应54°，则∠BCD
的度数为（）
| A．27° | B．54° | C．63° | D．36° |