端午节吃粽子是中华民族的传统习惯.小祥的妈妈从超市买了一些粽子回家,
用不透明袋子装着这些粽子(粽子除内部馅料不同外,其他一切相同),小祥问买了什么样的粽子,妈妈说:
“其中香肠馅粽子两个,剩余的都是绿豆馅粽子,若你从中任意拿出一个是香肠馅粽子的概率为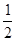 ”.
”.
(1)袋子中绿豆馅粽子有 个;
(2)小祥第一次任意拿出一个粽子(不放回),第二次再拿出一个粽子,请你用树状图或列表法,求小祥两次拿到的都是绿豆馅粽子的概率.
解方程组 .
如图,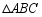 和
和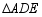 是有公共顶点的等腰直角三角形,
是有公共顶点的等腰直角三角形,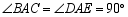 ,点
,点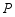 为射线
为射线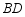 ,
,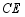 的交点.
的交点.
(1)求证: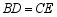 ;
;
(2)若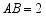 ,
,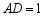 ,把
,把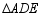 绕点
绕点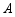 旋转,
旋转,
①当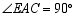 时,求
时,求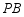 的长;
的长;
②直接写出旋转过程中线段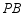 长的最小值与最大值.
长的最小值与最大值.
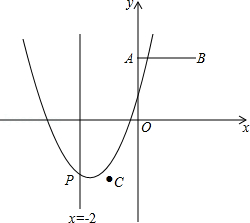
如图,已知点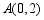 ,
, ,
,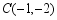 ,抛物线
,抛物线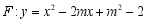 与直线
与直线 交于点
交于点 .
.
(1)当抛物线 经过点
经过点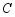 时,求它的表达式;
时,求它的表达式;
(2)设点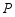 的纵坐标为
的纵坐标为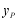 ,求
,求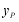 的最小值,此时抛物线
的最小值,此时抛物线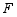 上有两点
上有两点 ,
,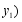 ,
, ,
, ,且
,且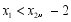 ,比较
,比较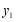 与
与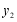 的大小;
的大小;
(3)当抛物线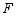 与线段
与线段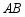 有公共点时,直接写出
有公共点时,直接写出 的取值范围.
的取值范围.
如图,在 中,
中, ,点
,点 在
在 上,以
上,以 为半径的
为半径的 交
交 于点
于点 ,
, 的垂直平分线交
的垂直平分线交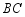 于点
于点 ,交
,交 于点
于点 ,连接
,连接 .
.
(1)判断直线 与
与 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若 ,
, ,
, ,求线段
,求线段 的长.
的长.

小李是某服装厂的一名工人,负责加工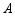 ,
,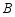 两种型号服装,他每月的工作时间为22天,月收入由底薪和计件工资两部分组成,其中底薪900元,加工
两种型号服装,他每月的工作时间为22天,月收入由底薪和计件工资两部分组成,其中底薪900元,加工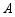 型服装1件可得20元,加工
型服装1件可得20元,加工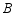 型服装1件可得12元.已知小李每天可加工
型服装1件可得12元.已知小李每天可加工 型服装4件或
型服装4件或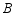 型服装8件,设他每月加工
型服装8件,设他每月加工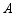 型服装的时间为
型服装的时间为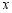 天,月收入为
天,月收入为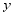 元.
元.
(1)求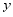 与
与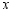 的函数关系式;
的函数关系式;
(2)根据服装厂要求,小李每月加工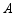 型服装数量应不少于
型服装数量应不少于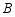 型服装数量的
,那么他的月收入最高能达到多少元?
型服装数量的
,那么他的月收入最高能达到多少元?