(文)在平面直角坐标系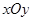 中,设锐角
中,设锐角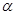 的始边与
的始边与 轴的非负半轴重合,终边与单位 圆交于点
轴的非负半轴重合,终边与单位 圆交于点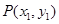 ,将射线
,将射线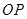 绕坐标原点
绕坐标原点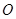 按逆时针方向旋转
按逆时针方向旋转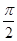 后与单位圆交于点
后与单位圆交于点 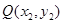 .记
.记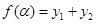 .(1)求函数
.(1)求函数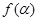 的值域;(2)设
的值域;(2)设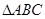 的角
的角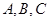 所对的边分别为
所对的边分别为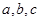 ,若
,若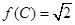 ,且
,且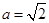 ,
,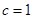 ,求
,求 .
.
已知焦点在x轴的椭圆的中心为坐标原点O,椭圆短半轴长为1,动点
 在直线
在直线 (
( 为长半轴,
为长半轴, 为半焦距)上.
为半焦距)上.
(1)求椭圆的标准方程;
(2)求以OM为直径且被直线 截得的弦长为2的圆的方程;
截得的弦长为2的圆的方程;
(3)设F是椭圆的右焦点,过点F作OM的垂线与以OM为直径的圆交于点N,求证:线段ON的长为定值,并求出这个定值
如图,已知四棱锥 底面
底面 为菱形,
为菱形, 平面
平面 ,
,
 、
、 分别是
分别是 、
、 的中点.
的中点.
(1)证明:
(2)设AB=2, 若 为线段
为线段 上的动点,
上的动点, 与平面
与平面 所
所 成的最大角的正切值为
成的最大角的正切值为 求二面角
求二面角 的余弦值.
的余弦值.
在棱长为1的正方体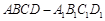 中,
中, 分别是棱
分别是棱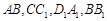 的中点.
的中点.
(1)证明: 平面
平面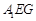 ;
;
(2)求三棱锥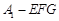 的体积.
的体积.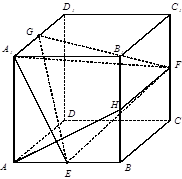
设计一个程序框图求 的值,并写出程序。
的值,并写出程序。
已知圆C: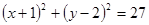 与
与
直线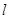 :
: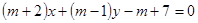 ,
,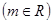
(1)证明:对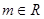 ,
,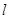 与圆C恒交于两点;
与圆C恒交于两点;
(2)求直线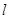 被圆C截得的线段最短长度,并求
被圆C截得的线段最短长度,并求 此时
此时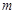 的值。
的值。