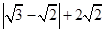喝绿茶前需要烧水和泡茶两个工序，即需要将电热壶中的水烧到100℃，然后停止烧水，等水温降低到适合的温度时再泡茶，烧水时水温
（℃）与时间菇（min）成一次函数关系；停止加热1分钟后（1分钟内水温不变），水壶中水的温度y（℃）与时间
（min）近似于反比例函数关系（如图）．已知水壶中水的初始温度是20℃，降温过程中水温不低于20℃．
（1）求出图中AB所在直线对应的函数关系式，并且写出自变量的取值范围；
（2）从水壶中的水烧开（100℃）降到80℃就可以进行泡制绿茶，问从水烧开到泡茶需要等待多长时间?
如图，在△ABC中，D是BC的中点，DE⊥AB于E，DF⊥AC于点F，且BE=CF.求证：AD平分∠BAC．
如图，点B，D，C，F在一条直线上，且BC＝FD，AB＝EF．
（1）请你只添加一个条件（不再加辅助线），使△ABC≌△EFD，你添加的条件是；
（2）添加了条件后，证明△ABC≌△EFD。
已知：如图，A、B是两个蓄水池，都在河流a的同侧，为了方便灌溉作物，要在河边建一个抽水站，将河水送到A、B两地，问该站建在河边什么地方，可使所修的渠道最短，试在图中确定该点（保留作图痕迹）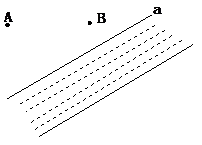
已知，如图，∠AOB的两边上的两点M、N，
求作：点P，使点P到OA、OB的距离相等，且PM=PN.（保留作图痕迹）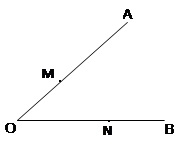
计算：