如图□ABCD的对角线AC，BD交于点O，AE平分∠BAD交BC于点E，且∠ADC=600，AB=
BC，连接OE ．下列 结论：①∠CAD=300 ② S□ABCD=AB•AC ③ OB=AB ④ OE=
BC 成立的个数有（ ）
| A．1个 | B．2个 | C．3个 | D．4个 |
如图，AB是⊙O的直径，弦CD⊥AB于点E，连接OC，若OC=5，CD=8，则tan∠COE=（）
A． |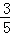
B． |
C． |
D． |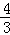
在下列实数：π，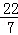
，tan30°，
，
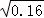，其中有理数的个数为（）
| A．1个 | B．2个 | C．3个 | D．4个 |
在△ABC中，若
|
|=0，且∠B，∠C都是锐角，则∠A的度数是（）
| A．15° | B．60° | C．75° | D．30° |
如图，点D是△ABC的边BC上一点，如果AB=AD=2，AC=4，且BD：DC=2：3，则△ABC是（）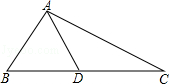
| A．锐角三角形 | B．直角三角形 |
| C．钝角三角形 | D．锐角三角形或直角三角形 |
已知α、β为锐角，若12sin2α+20cos2β﹣12sinα﹣20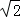
cosβ+13=0，则α+β等于（）
| A．60° | B．90° | C．105° | D．75° |