现有甲、乙两个容器，分别装有进水管和出水管，两容器的进出水速度不变，先打开乙容器的进水管，2分钟时再打开甲容器的进水管，又过2分钟关闭甲容器的进水管，再过4分钟同时打开甲容器的进、出水管．直到12分钟时，同时关闭两容器的进出水管，打开和关闭水管的时间忽略不计。容器中的水量y（升）与乙容器注水时间x之间的关系如图所示:
（1）求甲容器的进、出水速度．
（2）甲容器进、出水管都关闭后，是否存在两容器的水量相等。若存在，求出此时的时间．
（3）若使两容器第12分钟时水量相等，则乙容器6分钟后进水速度应变为多少？
（1）解方程：
（2）当
为何值时，关于
的方程
有两个实数根．
（1）计算: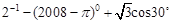
(2)
子求值。
如图，平面直角坐标系中，⊙P与x轴分别交于A、B两点，点P的坐标为（2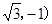
，AB=4
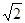，直线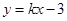
与x轴、y轴分别交于C 、D两点，∠OCD=60°
（1）设⊙P的半径为r，则r=
（2）求k的值.
（3）将⊙P沿直线x=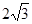
向下平移，当⊙P与直线CD相切于点E时，求点E的坐标.
某商场销售的一种进价为20元/台的台灯，经调查发现，该台灯每天的销售量w(台)与销售单价x(元)满足w=-2x+80，设销售这种台灯每天的利润为y（元）
(1)求y与x之间的函数关系式
(2)在保证销售量尽可能大的前提下，该商场每天想获得150元的利润，应将销售单价定为多少元？
如图，在△ABC中，AB=AC，以AB为直径的⊙O分别交AC、BC于点D、E，点F在AC的延长线上，且∠CBF=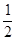
∠CAB
(1)求证：直线BF是⊙O的切线；
(2)若AB=5，BC=2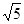
，求AD的长.