某电脑公司经销甲种型号电脑,受经济危机影响,电脑价格不断下降,今年三月份的电脑售价比去年同期每台降价1000元,如果卖出相同数量的电脑,去年销售额为10万元,今年销售额只有8万元.
(1)今年三月份甲种电脑每台售价多少元;
(2)为了增加收入电脑公司决定再经销乙种型号电脑.已知甲种每台进价3500元,乙种电脑每台进价3000元,公司预计用不少于4.8万元的资金购进这两种电脑共15台,则甲种电脑至少购进多少台.
如图,在Rt△ABC中,∠ACB=90°,AC=10cm,BC=5cm,点E从点C出发沿射线CA以每秒2cm的速度运动,同时点F从点B出发沿射线BC以每秒1cm的速度运动.设运动时间为t秒.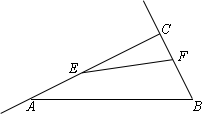
(1)填空:AB=cm;
(2)若0<t<5,试问:t为何值时,以E、C、F为顶点的三角形与△ABC相似;
(3)若∠ACB的平分线CG交△ECF的外接圆于点G.试探究在整个运动过程中,CE、CF、CG之间存在的数量关系,并说明理由.
如图,“和谐号”高铁列车的小桌板收起时,小桌板的支架底端与桌面顶端的距离OA=75厘米,且可以近似看作与地面垂直.展开小桌板使桌面保持水平,此时CB⊥AO,∠AOB=∠ACB=37°,且支架长OB与桌面宽BC的长度之和等于OA的长度.求小桌板桌面的宽度BC.(参考数据sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
学校举行数学知识竞赛,设立了一、二、三等奖,计划共购买45件奖品,其中二等奖奖品件数比一等奖奖品件数的2倍还少5件,已知购买一等奖奖品x件.各种奖品的单价如下表.
| 奖品 |
一等奖奖品 |
二等奖奖品 |
三等奖奖品 |
| 单价(元) |
12 |
10 |
8 |
(1)学校购买二等奖奖品件,三等奖奖品件;(用含x的代数式表示)
(2)若购买三等奖奖品的费用不超过二等奖奖品费用的2倍,学校为节省开支,应如何购买这三种奖品?总费用最少是多少元?
已知:如图,四边形ABCD和四边形AECF都是矩形,AE与BC交于点M,CF与AD交于点N.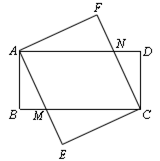
(1)求证:△ABM≌△CDN;
(2)矩形ABCD和矩形AECF满足何种关系时,四边形 AMCN是菱形,证明你的结论.
“低碳环保,你我同行”.两年来,扬州市区的公共自行车给市民出行带来切实方便.电视台记者在某区街头随机选取了市民进行调查,调查的问题是“您大概多久使用一次公共自行车?”,将本次调查结果归为四种情况:
| A.每天都用; | B.经常使用; | C.偶尔使用; | D.从未使用.将这次调查情况整理并绘制如下两幅统计图: |
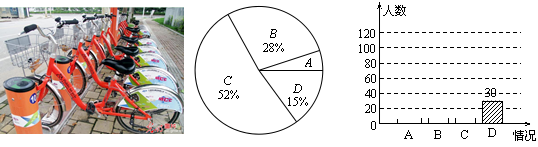
根据图中的信息,解答下列问题:
(1)本次活动共有位市民参与调查;
(2)补全条形统计图;
(3)根据统计结果,若该区有46万市民,请估算每天都用公共自行车的市民约有多少人?