某汽车制造厂开发了一款新式电动汽车，计划一年生产安装240辆。由于抽调不出足够的熟练工来完成新式电动汽车的安装，工厂决定招聘一些新工人，他们经过培训后上岗，也能独立进行进行电动汽车的安装。生产开始后，调研部门发现：1名熟练工和2名新工人每月可安装8辆电动汽车；2名熟练工和3名新工人每月可安装14辆电动汽车．
（1）每名熟练工和新工人每月分别可以安装多少辆电动汽车？
（2）如果工厂招聘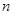
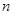（0＜＜10）名新工人，使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务(每月完成的量相同)，那么工厂有哪几种新工人的招聘方案？
（3）在（2）的条件下，工厂给安装电动汽车的每名熟练工每月发2000元的工资，给每名新工人每月发1200元的工资，那么工厂应招聘多少名新工人，使新工人的数量多于熟练工，同时工厂每月支出的工资总额W（元）尽可能的少？
如图，对称轴为直线x=﹣1的抛物线y=ax2+bx+c（a≠0）与x轴相交于A、B两点，其中点A的坐标为（﹣3，0）．
（1）求点B的坐标；
（2）已知a=1，C为抛物线与y轴的交点．
①若点P在抛物线上，且S△POC=4S△BOC．求点P的坐标；
②设点Q是线段AC上的动点，作QD⊥x轴交抛物线于点D，求线段QD长度的最大值．
某体育休闲超市购进一种成本为20元/个的风筝，据市场调查分析，若按25元/个销售，一个月能售出70个，在此基础上，售价每涨1元/个，月销售量就减少2个．设这种风筝的销售单价为x（元/个），该超市每月销售这种风筝的所获得的利润为y（元），针对这种风筝的销售情况，请解答下列问题:
（1）用含x的代数式分别表示出每个风筝的销售利润为 元，每月卖出的风筝的个数是 个；
（2）求y与x之间的函数关系式；
（3）若该超市想在每月销售这种风筝的成本不超过800元的情况下，使得月销售利润达到600元，则每个风筝的售价应定为多少元?
如图：AB是⊙O的直径，以OA为直径的⊙O1与⊙O的弦AC相交于D，DE⊥OC，垂足为E。
（1）求证：AD＝DC
（2）求证：DE是的切线
（3）如果OE＝EC，请判断四边形O1OED是什么四边形，并证明你的结论。
已知：如图，在△ABC中，∠BAC=1200，以BC为边向形外作等边三角形△BCD，把△ABD绕着点D按顺时针方向旋转600后得到△ECD，若AB=3，AC=2，求∠BAD的度数与AD的长．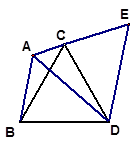
已知关于
的方程
有两个不相等的实数根
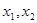（1）求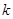
的取值范围．（2）是否存在实数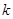使方程的两实数根互为相反数？如果存在，求出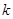的值，如果不存在，请说明理由．