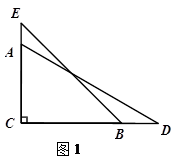
如图1，小明将一副直角三角尺的直角顶点C叠放在一起．若保持三角尺BCE（其中∠EBC=45°）不动，三角尺ACD的CD边与CB边重合，然后将三角尺ACD（其中
∠ADC=30°）绕点C按逆时针方向任意转动一个角度∠BCD．
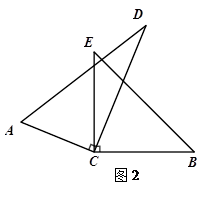
（1）如图2，若∠ECD =25°，则∠ACB= ；若∠ACB=130°，则∠ECD = ．
（2）①当三角尺ACD绕直角顶点C旋转到如图2的位置时，猜想∠ACB与∠DCE的数量关系为 ；
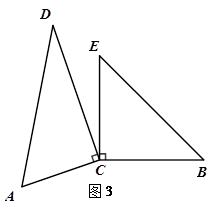
②当三角尺ACD绕直角顶点C旋转到如图3的位置时，上述关系是否依然成立，请说明理由．
（3）设∠BCD=α（0°＜α＜180°）
①∠ACB能否是∠DCE的4倍？若能求出α的值；若不能说明理由．
②在旋转过程中，若AD与三角尺BCE的一条边平行，请求出α的所有可能值．
.
的值(1)为正；(2)值为负；(3)值为0.
； (2)
.
，
，
，
，
，π，
.