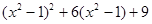【问题情境】如图1,在△ABC中,AB=AC,点P为边BC上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D、E,过点C作CF⊥AB,垂足为F.求证:PD+PE=CF.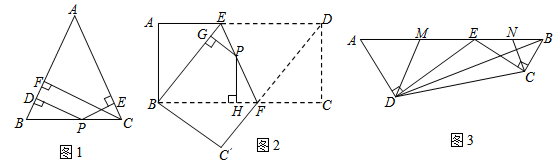
【结论运用】如图2,将矩形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P为折痕EF上的任一点,过点P作PG⊥BE、PH⊥BC,垂足分别为G、H,若AD=8,CF=3,求PG+PH的值;
【迁移拓展】图3是一个航模的截面示意图.在四边形ABCD中,E为AB边上的一点,ED⊥AD,EC⊥CB,垂足分别为D、C,且AD·CE=DE·BC,AB=8,AD=3,BD=7;M、N分别为AE、BE的中点,连接DM、CN,求△DEM与△CEN的周长之和.
图①是一个长为2a,宽为2b的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的形状拼成一个正方形.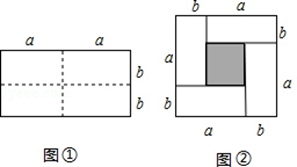
(1)图②中阴影部分的正方形的边长是 _________ ;
(2)请用两种不同的方法求图2中阴影部分的面积:
方法1: _________ ;
方法2: _________ ;
(3)观察图②,请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 _________ ;
(4)根据(3)中的等量关系解决如下问题:若m﹣n=﹣5,mn=3,则(m+n)2的值为多少?
某农户以前在山上种了脐橙果树44株,前两年已有所收获。现进入第三年收获期。收获时,先随意采摘5株果树上的脐橙,称得每株果树上的脐橙质量如下(单位:千克):35,35,34,39,37
(1)根据样本平均数估计,这年脐橙的总产量约是多少?
(2)若市场上的脐橙售价为每千克5元,则这年该农户卖脐橙的收入将达多少元?
(3)已知该农户第一年卖脐橙的收入为5500元,根据以上估算,试求第二年、第三年卖脐橙收入的年平均增长率是多少?
为极大地满足人民生活的需求,丰富市场供应,我市淮上区温棚种植面积在不断扩大.在耕地上培成一行一行的长方形土埂,按顺序间隔种植不同农作物的方法叫分垄间隔套种。科学研究表明:在塑料温棚中分垄间隔套种高、矮不同的蔬菜和水果,可增加它们的光合作用,提高单位面积的产量和经济效益。现有一个种植总面积为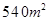 的长方形塑料温棚,分垄间隔套种草莓和西红柿共
的长方形塑料温棚,分垄间隔套种草莓和西红柿共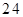 垄,种植的草莓或西红柿单种农作物的总垄数不低于
垄,种植的草莓或西红柿单种农作物的总垄数不低于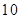 垄,又不超过
垄,又不超过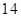 垄(垄数为正整数),它们的占地面积、产量、利润分别如下:
垄(垄数为正整数),它们的占地面积、产量、利润分别如下:
(1)若设草莓共种植了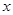 垄,通过计算说明共有几种种植方案?分别是哪几种?
垄,通过计算说明共有几种种植方案?分别是哪几种?
(2)在这几种种植方案中,哪种方案获得的利润最大?最大利润是多少?
先化简再求值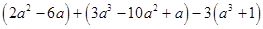 ,其中
,其中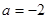
因式分解:(1)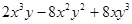 (2)
(2)