（本题10分）如图，在平面直角坐标系中，点O为坐标原点，直线y=kx+1（k≠0）与x轴交于点A，与y轴交于点C，过点C的抛物线y=ax2-（6a-2）x+b （a≠0）与直线AC交于另一点B，点B坐标为（4，3）．
（1）求a的值；
（2）点p是射线CB上的一个动点，过点P在作PQ⊥x轴，垂足为点Q，在x轴上点Q的右侧取点M，使MQ=
，在QP的延长线上取点N，连接PM，AN，已知tan∠NAQ-tan∠MPQ=
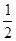，求线段PN的长；
（3）在（2）的条件下，过点C作CD⊥AB，使点D在直线AB 下方，且CD=AC，连接PD，NC，当以PN，PD，NC的长为三边长构成的三角形面积是
时，在y轴左侧的抛物线上是否存在点E，连接NE，PE，使得ΔENP与以PN、PD、NC的长为三边长的三角形全等？若存在，求出点E坐标；若不存在，请说明理由．
如图，平行四边形ABCD中，AE：EB=1：2，求△AEF与△CDF的周长的比．如果S△AEF=6cm2，
求S△CDF．
国民体质监测中心等机构开展了青少年形体测评．专家组随机抽查了某市若干名初中学生坐姿、站姿、走姿的好坏情况．我们对专家的测评数据作了适当处理（如果一个学生有一种以上不良姿势，我们以他最突出的一种作记载），并将统计结果绘制了如下两幅不完整的统计图，请你根据图中所给信息解答下列问题：
（1）请将两幅统计图补充完整；
（2）在这次形体测评中，一共抽查了 名学生，如果全市有10万名初中生，那么全市初中生中，三姿良好的学生约有 人；
（3）根据统计结果，请你简单谈谈自己的看法．
（1）计算：|﹣
|﹣（﹣4）﹣1+（
）0﹣2cos30°
（2）先化简，再求值，（
﹣
）÷，其中a=
+1．
如图1，点A、B在数轴上分别表示有理数a、b，A、B两点之间的距离表示为AB，在数轴上A、B两点之间的距离AB=|a﹣b|．利用数形结合思想回答下列问题：
（1）数轴上表示1和5两点之间的距离是 ，数轴上表示2和﹣1的两点之间的距离是 ；
（2）数轴上表示x和﹣1的两点之间的距离表示为 ；
（3）若x表示一个有理数，化简：|x﹣2|+|x+4|；
（4）利用数轴求出|x+3|+|x﹣4|的最小值，并写出此时x可取哪些整数值？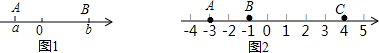
观察下列等式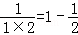
，
，
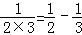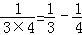，以上三个等式两边分别相加得：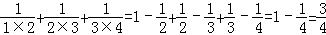
（1）猜想并写出：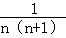
=
﹣
；
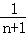（2）计算：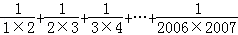
= ；
（3）探究并计算：
= ；
（4）若|ab﹣3|与|b﹣1|互为相反数，求：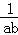
+
+
+
…+
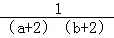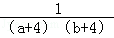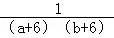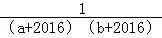的值．