阅读理解:如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”.
应用:在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点C的极坐标应记为( )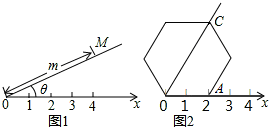
| A.(60°,4) | B.(45°,4) |
C.(60°,2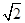 ) ) |
D.(50°,2 ) ) |
甲、乙两人赛跑,所跑路程与时间的关系如图(实线为甲的路程与时间的关系图象,虚线为乙的路程与时间的关系图象),小王根据图象得到如下四条信息,其中错误的是( )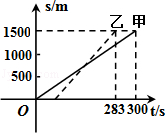
| A.这是一次1500m赛跑 |
| B.甲、乙同时起跑 |
| C.甲、乙两人中先到达终点的是乙 |
| D.甲在这次赛跑中的速度为5m/s |
顺次连结四边形ABCD各边中点得到的四边形一定是( )
| A.矩形 | B.正方形 | C.平行四边形 | D.菱形 |
如图,如果张力的位置可表示为(1,3),则王红的位置应表示为( )
| A.(4,1) | B.(4,2) | C.(2,4) | D.(3,4) |
已知一次函数y=kx+b(k≠0)的草图如图所示,则下列结论正确的是( )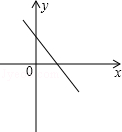
| A.k>0,b>0 | B.k>0,b<0 | C.k<0,b>0 | D.k<0,b<0 |
菱形的两条对角线长分别为6cm、8cm,则它的面积为( )cm2.
| A.6 | B.12 | C.24 | D.48 |