给出定义，若一个四边形中存在相邻两边的平方和等于一条对角线的平方，则称该四边形为勾股四边形．
（1）在你学过的特殊四边形中，写出两种勾股四边形的名称；
（2）如图，将△ABC绕顶点B按顺时针方向旋转60°得到△DBE，连接AD，DC，CE，已知∠DCB=30°．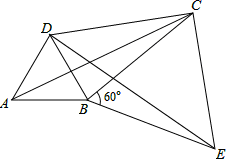
①求证：△BCE是等边三角形；
②求证：DC2+BC2=AC2，即四边形ABCD是勾股四边形．
已知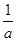
－
＝
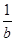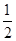，求
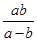的值．
阅读下列材料，你能得到什么结论？并利用(1)的结论分解因式．
(1)形如x2＋(p＋q)x＋pq型的二次三项式，有以下特点：①二次项系数是1；②常数项是两个数之积；③一次项系数是常数项的两个因数之和，把这个二次三项式进行分解因式，可以这样来解：
x2＋(p＋q)x＋pq＝x2＋px＋qx＋pq
＝(x2＋px)＋(qx＋pq)＝x(x＋p)＋q(x＋p)
＝(x＋p)(x＋q)．
因此，可以得x2＋(p＋q)x＋pq＝________．
利用上面的结论，可以直接将某些二次项系数为1的二次三项式分解因式．
(2)利用(1)的结论分解因式：
①m2＋7m－18；
②x2－2x－15.
已知
＋
＝
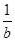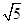(a≠b)，求
－
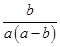的值．
先化简，再求值：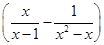
÷(x＋1)其中x＝
.
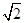先化简、再求值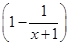
÷
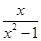，其中x＝
＋1.