如图,飞机沿水平方向(A、B两点所在直线)飞行,前方有一座高山,为了避免飞机飞行过低,就必须测量山顶M到飞行路线AB的距离MN.飞机能够测量的数据有俯角和飞行的距离(因安全因素,飞机不能飞到山顶的正上方N处才测飞行距离),请设计一个距离MN的方案,要求:
(1)指出需要测量的数据(用字母表示,并在图中标出);
(2)用测出的数据写出求距离MN的步骤.
 |
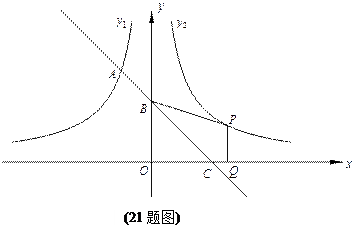
如图,一次函数的图象与反比例函数y1=" –" ( x<0)的图象相交于A点,与y轴、x轴分别相交于B、C两点,且C(2,0).当x<–1时,一次函数值大于反比例函数的值,当x>–1时,一次函数值小于反比例函数值.
(1)求一次函数的解析式;
(2)设函数y2= (x>0)的图象与y1=" –" (x<0)的图象关于y轴对称.在y2= (x>0)的图象上取一点P(P点的横坐标大于2),过P作PQ⊥x轴,垂足是Q,若四边形BCQP的面积等于2,求P点的坐标.
 |
某县为鼓励失地农民自主创业,在2010年对60位自主创业的失地农民自主创业的失地农民进行奖励,共计划奖励10万元.奖励标准是:失地农民自主创业连续经营一年以上的给予1000元奖励;自主创业且解决5人以上失业人员稳定就业一年以上的,再给予2000元奖励.问:该县失地农民中自主创业连续经营一年以上的和自主创业且解决5人以上失业人员稳定就业一年以上的农民分别有多少人?
某校开展了以“人生观、价值观”为主题的班队活动,活动结束后,初三(2)班数学兴趣小组提出了5个主要观点并在本班50名学生中进行了调查(要求每位同学只选自己最认可的一项观点),并制成了如下扇形统计图.
(1)该班学生选择“和谐”观点的有 人,在扇形统计图中,“和谐”观点所在扇形区域的圆心角是 度.
(2)如果该校有1500名初三学生,利用样本估计选择“感恩”观点的初三学生约有 人.
(3)如果数学兴趣小组在这5个主要观点中任选两项观点在全校学生中进行调查,求恰好选到“和谐”和“感恩”观点的概率(用树状图或列表法分析解答)
 |
解不等式组 ,并把它的解集在数轴上表示出来.
,并把它的解集在数轴上表示出来.